Hướng dẫn Giải bài tập Toán 10 Chân trời sáng tạo Chương 5 Bài 3 Tích của một số với một vectơ giúp các em học sinh nắm vững phương pháp giải bài tập và ôn luyện tốt kiến thức.
-
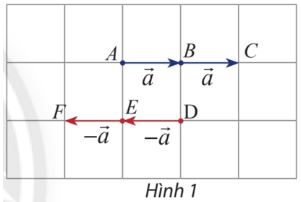
Hoạt động khám phá 1 trang 94 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)
-
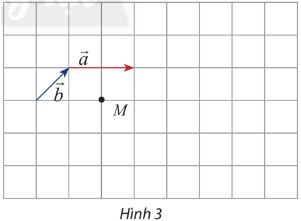
Thực hành 1 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hai vectơ cho hai vectơ \(\overrightarrow a ,\overrightarrow b \) và điểm M như hình 3.
a) Hãy vẽ vectơ \(\overrightarrow {MN} = 3\overrightarrow a ,\overrightarrow {MP} = - 3\overrightarrow b \)
b) Cho biết mỗi ô có cạnh bằng 1. Tính: \(\left| {3\overrightarrow b } \right|,\left| { - 3\overrightarrow b } \right|,\left| {2\overrightarrow a + 2\overrightarrow b } \right|\).
-
Thực hành 2 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
-
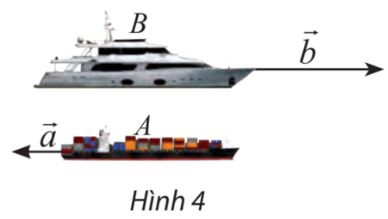
Vận dụng trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Một con tàu chở hàng A đang đi về hướng tây với tốc độ 20 hải lý/ giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lý/giờ. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của tàu B theo vectơ vận tốc \(\overrightarrow a \) của tòa A.
- VIDEOYOMEDIA
-
Hoạt động khám phá 2 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) cùng phương khác \(\overrightarrow 0 \) và cho \(\overrightarrow c = \frac{{\left| {\overrightarrow a } \right|}}{{\left| {\overrightarrow b } \right|}}.\overrightarrow b \). So sánh độ dài và hướng của hai vectơ \(\overrightarrow a \) và \(\overrightarrow c \)
-
Thực hành 3 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \). Chứng minh ba điểm I, G, J thẳng hàng
-
Giải bài 1 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
a) \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MO} \)
b) \(\overrightarrow {AB} + \overrightarrow {AC} + \overrightarrow {AD} = 2\overrightarrow {AC} \)
-
Giải bài 2 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tứ giác ABCD gọi M và N lần lượt là trung điểm của các cạnh AB và CD . Chứng minh rằng
a) \(\overrightarrow {AC} + \overrightarrow {BD} = 2\overrightarrow {MN} \)
b) \(\overrightarrow {AC} + \overrightarrow {BD} = \overrightarrow {BC} + \overrightarrow {AD} \)
-
Giải bài 3 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hai điểm phân biệt A và B. Xác định điểm M sao cho \(\overrightarrow {MA} + 4\overrightarrow {MB} = \overrightarrow 0 \)
-
Giải bài 4 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} + \overrightarrow {MD} = 4\overrightarrow {MG} \)
-
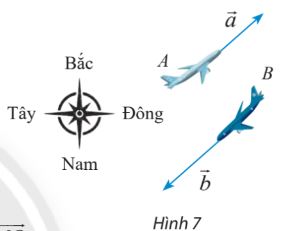
Giải bài 5 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Máy bay A đang bay về hướng Đông Bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng Tây Nam với tốc độ 800 km/h. Biểu diễn vectơ vận tốc \(\overrightarrow b \)của máy bay B theo vectơ vận tốc \(\overrightarrow a \) của máy bay A
-
Giải bài 6 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho 2 điểm phân biệt A và B
a) Xác định điểm O sao cho \(\overrightarrow {OA} + 3\overrightarrow {OB} = \overrightarrow 0 \)
b) Chứng minh rằng với mọi điểm M, ta có \(\overrightarrow {MA} + 3\overrightarrow {MB} = 4\overrightarrow {MO} \)
-
Giải bài 7 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho tam giác ABC
a) Xác định các điểm M, N, P thỏa mãn: \(\overrightarrow {MB} = \frac{1}{2}\overrightarrow {BC} ,\overrightarrow {AN} = 3\overrightarrow {NB} ,\overrightarrow {CP} = \overrightarrow {PA} \)
b) Biểu thị mỗi vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} \) theo hai vectơ \(\overrightarrow {BC} ,\overrightarrow {BA} \)
c) Chứng minh ba điểm M, N, P thẳng hàng
-
Giải bài 1 trang 96 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hình bình hành ABCD có G là trọng tâm của tam giác ABD. Chứng minh rằng: \(\overrightarrow {AC} = 3\overrightarrow {AG} \)
-
Giải bài 2 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Gọi AM là trung tuyến của tam giác ABC và D là trung điểm của đoạn AM. Chứng minh rằng:
a) \(2\overrightarrow {DA} + \overrightarrow {DB} + \overrightarrow {DC} = \overrightarrow 0 \)
b) \(2\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = 4\overrightarrow {OD} \) với O là điểm tùy ý
-
Giải bài 3 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Lấy một điểm M tùy ý. Chứng minh rằng:
a) I là trung điểm của đoạn thẳng AB khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \)
b) G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
-
Giải bài 4 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho hai điểm phân biệt A và B. Tìm điểm K sao cho \(3\overrightarrow {KA} + 2\overrightarrow {KB} = \overrightarrow 0 \).
-
Giải bài 5 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Cho lục giác ABCDEF. Gọi M, N, P, Q, R, S lần lượt là trung điểm của các cạnh AB, BC, CD, DE, EF, FA. Chứng minh rằng hai tam giác MPR và NQS có cùng trọng tâm.
-
Giải bài 6 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Máy bay A bay với vận tốc \(\overrightarrow a \), máy bay B bay cùng hướng có vận tốc chỉ bằng một nửa máy A. Biểu diễn vectơ vận tốc \(\overrightarrow b \) của máy bay B theo vectơ vận tốc \(\overrightarrow a \)của máy bay A.