Thực hành 2 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1
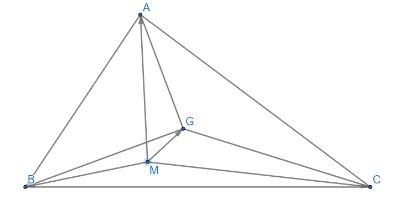
Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \)
Hướng dẫn giải chi tiết Thực hành 2
Phương pháp giải
Sử dụng quy tắc 3 điểm \(\overrightarrow {MA} = \overrightarrow {MG} + \overrightarrow {GA}\)
Lời giải chi tiết
\(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = 3\overrightarrow {MG} \Leftrightarrow \overrightarrow {MG} + \overrightarrow {GA} + \overrightarrow {MG} + \overrightarrow {GB} + \overrightarrow {MG} + \overrightarrow {GC} = 3\overrightarrow {MG} \)
\( \Leftrightarrow \left( {\overrightarrow {MG} + \overrightarrow {MG} + \overrightarrow {MG} } \right) + \left( {\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} } \right) = 3\overrightarrow {MG} \)
\( \Leftrightarrow 3\overrightarrow {MG} = 3\overrightarrow {MG} \) (đpcm) ( Vì G là trọng tâm của tam giác ABC nên \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \))
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Hoạt động khám phá 1 trang 94 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 96 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Cho tam giác \(ABC\) và điểm \(G\). Hãy chứng minh rằng: Nếu có điểm \(O\) sao cho \(\overrightarrow {OG} = \dfrac{1}{3}\left( {\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} } \right)\) thì \(G\) là trọng tâm tam giác \(ABC\).
bởi Vũ Hải Yến
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời