Hoạt động khám phá 1 trang 94 SGK Toán 10 Chân trời sáng tạo tập 1
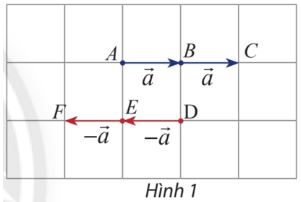
Cho vectơ \(\overrightarrow a \). Hãy xác định độ dài và hướng của hai vectơ \(\overrightarrow a + \overrightarrow a ,\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)\): (Hình 1)
Hướng dẫn giải chi tiết Hoạt động khám phá 1
Phương pháp giải
+) Tích của một số thực \(k\)với một vecto \(\overrightarrow a \ne \overrightarrow 0 \) là một vecto, kí kiệu là \(k\overrightarrow a .\)
+) Vecto \(k\overrightarrow a \) có độ dài bằng \(\left| k \right|\left| {\overrightarrow a } \right|\) và cùng hướng với vecto \(\overrightarrow a \) nếu \(k > 0\), ngược hướng với vecto \(\overrightarrow a \) nếu \(k < 0\)
Lời giải chi tiết
Dựa vào hình 1 ta thấy
Vectơ \(\overrightarrow a + \overrightarrow a = \overrightarrow {AC} \) có độ dài bằng 2 lần vectơ \(\overrightarrow a \)và cùng hướng với vectơ \(\overrightarrow a \)
Vectơ \(\left( { - \overrightarrow a } \right) + \left( { - \overrightarrow a } \right)= \overrightarrow {DF}\) có độ dài bằng 2 lần vectơ \(\left( { - \overrightarrow a } \right)\) và cùng hướng với vectơ \(\left( { - \overrightarrow a } \right)\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Thực hành 1 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng trang 95 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 96 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 97 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 96 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 97 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Hãy chứng minh rằng nếu \(G\) và \(G'\) lần lượt là trọng tâm tam giác \(ABC\) và tam giác \(A'B'C'\) thì \(3\overrightarrow {G{G'}} = \overrightarrow {A{A'}} + \overrightarrow {B{B'}} + \overrightarrow {C{C'}} .\) Từ đó hãy suy ra điều kiện cần và đủ để hai tam giác \(ABC\) và \(A'B'C'\) có trọng tâm trùng nhau.
bởi thi trang
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời