Giải bài tập Toán 10 Cánh Diều Bài 5: Tích của một số với một vectơ

Gọi B là trung điểm của AC.

Chứng tỏ rằng \(\overrightarrow {AC}  = \overrightarrow {AB}  + \overrightarrow {AB} \). 

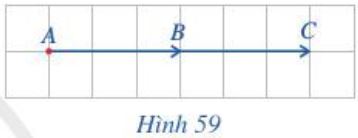
Quan sát vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)$\stackrel{}{}$, nêu mối liên hệ về hướng và độ dài của vectơ 2\(\overrightarrow {AB} \)$\stackrel{}{}$ với \(\overrightarrow {AB} \)$\stackrel{}{}$.

Cho tam giác ABC. Hai đường trung tuyến AM và BN cắt nhau tại G.

Tìm các số a, b biết: \(\overrightarrow {AG}  = a.\overrightarrow {AM} ;\overrightarrow {GN}  = b.\overrightarrow {GB} \)

Cho ba điểm A, B, C. Chứng minh \(3\left( {\overrightarrow {AB}  + 2\overrightarrow {BC} } \right) - 2\left( {\overrightarrow {AB}  + 3\overrightarrow {BC} } \right) = \overrightarrow {AB} \)

Cho I là trung điểm của đoạn thẳng AB và điểm M tùy ý. Chứng minh rằng \(\overrightarrow {MA\;}  + \;\overrightarrow {MB\;}  = \;\overrightarrow {2MI} \;\) 

Cho G là trọng tâm của tam giác ABC và điểm M tùy ý. Chứng minh rằng \(\overrightarrow {MA}  + \overrightarrow {MB}  + \overrightarrow {MC}  = 3\overrightarrow {MG} \). 

Cho tam giác ABC có G là trọng tâm. Chứng minh \(\overrightarrow {AB}  + \overrightarrow {AC}  = 3\overrightarrow {AG} .\)

Cho hai vectơ \(\overrightarrow a\) và \(\overrightarrow b\)$\stackrel{}{}$ khác \(\overrightarrow 0\) sao cho \(\vec a = k\vec b\) với k là số thực khác 0. Nêu nhận xét về phương của hai vectơ \(\overrightarrow a\)$\stackrel{}{}$ và \(\overrightarrow b\).

Cho ba điểm phân biệt A, B, C.

a) Nếu ba điểm A, B, C thẳng hàng thì hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương hay không?

b) Ngược lại, nếu hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} \) cùng phương thì ba điểm A, B, C có thẳng hàng hay không?

Ở hình 61, tìm k trong mỗi trường hợp sau:

a) \(\overrightarrow {AC}  = k.\overrightarrow {AD} \)

b) \(\overrightarrow {BD}  = k.\overrightarrow {DC} \)

Cho hình thang MNPQ, MN // PQ, MN = 2PQ. Phát biểu nào sau đây là đúng?

A. \(\overrightarrow {MN}  = 2\overrightarrow {PQ} \)

B. \(\overrightarrow {MN}  = 2\overrightarrow {NP} \)

C. \(\overrightarrow {MN}  =  - 2\overrightarrow {PQ} \)

D. \(\overrightarrow {MQ}  =  - 2\overrightarrow {NP} \)

Cho đoạn thẳng AB = 6 cm.

a) Xác định điểm C thỏa mãn \(\overrightarrow {AC}  = \frac{1}{2}\overrightarrow {AB} \)

b) Xác định điểm D thỏa mãn \(\overrightarrow {AD}  =  - \frac{1}{2}\overrightarrow {AB} \)

Cho tam giác ABC có M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh:

a) \(\overrightarrow {AP}  + \frac{1}{2}\overrightarrow {BC}  = \overrightarrow {AN} \)

b) \(\overrightarrow {BC}  + 2\overrightarrow {MP}  = \overrightarrow {BA} \)

Cho tam giác ABC. Các điểm D, E thuộc cạnh BC thỏa mãn BD = DE = EC (Hình 62). Giả sử \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AC}  = \overrightarrow b .\) Biểu diễn các vecto \(\overrightarrow {BC} ,\overrightarrow {BD} ,\overrightarrow {BE} ,\overrightarrow {AD} ,\overrightarrow {AE} \) theo \(\overrightarrow a ,\overrightarrow b .\) 

Cho tứ giác ABCD có M, N lần lượt là trung điểm của hai cạnh AB và CD. Gọi G là trung điểm của đoạn thẳng MN, E là trọng tâm tam giác BCD. Chứng minh:

a) \(\overrightarrow {EA}  + \overrightarrow {EB}  + \overrightarrow {EC}  + \overrightarrow {ED}  = 4\overrightarrow {EG} \)

b) \(\overrightarrow {EA}  = 4\overrightarrow {EG} \)

c) Điểm G thuộc đoạn thẳng AE và \(\overrightarrow {AG}  = \frac{3}{4}\overrightarrow {AE} \)

Cho ABCD là hình bình hành. Đặt \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AD}  = \overrightarrow b .\) Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto \(\overrightarrow {AG} ,\overrightarrow {CG} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b .\) 

Cho tam giác ABC. Các điểm D, E, H thỏa mãn

\(\overrightarrow {DB}  = \frac{1}{3}\overrightarrow {BC} ,\;\overrightarrow {AE}  = \frac{1}{3}\overrightarrow {AC} ,\;\overrightarrow {AH}  = \frac{2}{3}\overrightarrow {AB} .\)

a) Biểu thị mỗi vecto \(\overrightarrow {AD} ,\overrightarrow {DH} ,\overrightarrow {HE} \) theo hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} .\)

b) Chứng minh D, E, H thẳng hàng.

Cho đoạn thẳng AB và O là trung điểm của AB. Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {AB}  = 2\overrightarrow {OA} \)  

B. \(\overrightarrow {AB}  = 2\overrightarrow {OB} \)  

C. \(\overrightarrow {AB}  =  - 2\overrightarrow {OB} \)

D. \(\overrightarrow {AO}  = 2\overrightarrow {AB} \)

Cho tam giác ABC và M là trung điểm của BC, G là trọng tâm của tam giác. Khẳng định nào sau đây đúng?

A. \(\overrightarrow {AM}  =  - 3\overrightarrow {GM} \)         

B. \(\overrightarrow {AM}  = \frac{3}{2}\overrightarrow {GM} \)           

C. \(\overrightarrow {AM}  =  - \frac{3}{2}\overrightarrow {GM} \)         

D. \(\overrightarrow {AM}  = 3\overrightarrow {GM} \)

Cho \(\overrightarrow a  \ne \overrightarrow 0 \). Khẳng định nào sau đây là sai?

A. \(\overrightarrow a \) và \(4\overrightarrow a \) cùng phương

B. \(\overrightarrow a \) và \( - 4\overrightarrow a \) cùng phương           

C. \(\overrightarrow a \) và \(4\overrightarrow a \) không cùng hướng

D. \(\overrightarrow a \) và \( - 4\overrightarrow a \) ngược hướng           

Cho đoạn thẳng AB và điểm C nằm giữa hai điểm A, B. Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {AC}  = \frac{{AC}}{{AB}}\overrightarrow {AB} \)           

B. \(\overrightarrow {AC}  =  - \frac{{AC}}{{AB}}\overrightarrow {AB} \)

C. \(\overrightarrow {AC}  = \frac{{AB}}{{AC}}\overrightarrow {AB} \)

D. \(\overrightarrow {AC}  =  - \frac{{AB}}{{AC}}\overrightarrow {AB} \)

Cho đoạn thẳng BC và điểm A nằm giữa hai điểm B, C. Khẳng định nào sau đây là đúng?

A. \(\overrightarrow {AC}  = \frac{{AC}}{{AB}}\overrightarrow {AB} \)

B. \(\overrightarrow {AC}  =  - \frac{{AC}}{{AB}}\overrightarrow {AB} \)

C. \(\overrightarrow {AC}  = \frac{{AB}}{{AC}}\overrightarrow {AB} \)

D. \(\overrightarrow {AC}  =  - \frac{{AB}}{{AC}}\overrightarrow {AB} \)

Cho tam giác ABC. Xác định các điểm M, N, P trong môi trường hợp sau:

a) \(\overrightarrow {AM}  = \overrightarrow {CB} \)    

b) \(\overrightarrow {AN}  =  - \frac{1}{2}\left( {\overrightarrow {AB}  + \overrightarrow {AC} } \right)\)

c) \(\overrightarrow {PA}  - \overrightarrow {PB}  + 2\overrightarrow {PC}  = \overrightarrow 0 \)

Cho tam giác ABC, kẻ phân giác AD. Đặt AB = c, AC = b. Chứng minh:

\(b\overrightarrow {DB}  + c\overrightarrow {DC}  = \overrightarrow 0 \) (*)

Cho hình bình hành ABCD. Lấy các điểm M, N, P thoả mãn \(\overrightarrow {AM}  = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN}  = \frac{1}{5}\overrightarrow {AC} ,\overrightarrow {AP}  = \frac{1}{3}\overrightarrow {AD} \). Đặt \(\overrightarrow {AB}  = \overrightarrow a ,\overrightarrow {AD}  = \overrightarrow b \). Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {MN} ,\overrightarrow {NP} \) theo các vectơ \(\overrightarrow a ,\overrightarrow b \) và chứng minh ba điểm M, N, P thẳng hàng.

Cho tam giác ABC. Lấy các điểm D, E, M, N thoả mãn \(\overrightarrow {AD}  = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {AE}  = \frac{2}{5}\overrightarrow {AC} ,\overrightarrow {BM}  = \frac{1}{3}\overrightarrow {BC} ,\overrightarrow {AN}  = k\overrightarrow {AM} \)

với k là số thực. Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {DE} ,\overrightarrow {EN} \) theo các vectơ \(\overrightarrow a  = \overrightarrow {AB} ,\overrightarrow b  = \overrightarrow {AC} \) và tìm k để ba điểm D, E, N thẳng hàng.

Cho tam giác ABC. Lấy các điểm A', B', C' không trùng với đỉnh của tam giác và lần lượt thuộc các cạnh AB, BC, CA thoả mãn \(\frac{{AA'}}{{AB}} = \frac{{BB'}}{{BC}} = \frac{{CC'}}{{CA}}\). Chứng minh hai tam giác ABC và A'B'C' có cùng trọng tâm.