Giải bài 6 trang 92 SGK Toán 10 Cánh diều tập 1
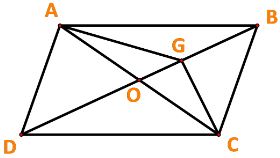
Cho ABCD là hình bình hành. Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b .\) Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto \(\overrightarrow {AG} ,\overrightarrow {CG} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b .\)
Hướng dẫn giải chi tiết Bài 6
Phương pháp giải
Quy tắc cộng: \(\overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD} \) với B, A, D bất kì.
Bước 1: Biểu diễn vecto \(\overrightarrow {BD} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b .\)
Bước 2: Biểu diễn vecto \(\overrightarrow {BG} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b \) dựa vào đẳng thức \(\overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} \)
Bước 3: Biểu thị các vecto \(\overrightarrow {AG} ,\overrightarrow {CG} \) theo vecto \(\overrightarrow {BG} \) và \(\overrightarrow a ,\overrightarrow b .\)
Hướng dẫn giải
Gọi O là giao điểm của AC và BD.
Ta có:
\(\overrightarrow {BA} + \overrightarrow {AD} = \overrightarrow {BD} \). Mà \(\overrightarrow {BA} = - \overrightarrow {AB} = - \overrightarrow a ;\overrightarrow {AD} = \overrightarrow b .\)
\( \Rightarrow \overrightarrow {BD} = - \overrightarrow a + \overrightarrow b \).
\(\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {AD} + \overrightarrow {BG} = \overrightarrow b + \overrightarrow {BG} ;\end{array}\)(*)
Lại có: \(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)
\( \Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)\)
Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = \overrightarrow b + \overrightarrow {BG} = \overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b ;\end{array} \right.\)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a + \frac{2}{3}\overrightarrow b .\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 4 trang 92 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 5 trang 92 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 7 trang 92 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 47 trang 99 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 48 trang 99 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 49 trang 99 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 50 trang 99 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 51 trang 99 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 52 trang 100 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 53 trang 100 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 54 trang 100 SBT Toán 10 Cánh diều tập 1 - CD
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.