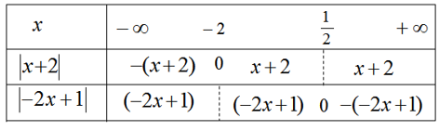Giải bài 4.42 tr 113 SBT Toán 10
Giải bất phương trình sau: |x + 2| + |-2x + 1| ≤ x + 1
Hướng dẫn giải chi tiết
Bảng xét dấu các giá trị tuyệt đối trong bất phương trình:
\left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \le - 2\\
- \left( {x + 2} \right) + \left( { - 2x + 1} \right) \le x + 1
\end{array} \right.\\
\left\{ \begin{array}{l}
- 1 < x \le \frac{1}{2}\\
\left( {x + 2} \right) + \left( { - 2x + 1} \right) \le x + 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x > \frac{1}{2}\\
\left( {x + 2} \right) - \left( { - 2x + 1} \right) \le x + 1
\end{array} \right.
\end{array} \right.\\
\Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \le - 2\\
4x \ge - 2
\end{array} \right.\\
\left\{ \begin{array}{l}
- 1 < x \le \frac{1}{2}\\
2x \ge 2
\end{array} \right.\\
\left\{ \begin{array}{l}
x \ge \frac{1}{2}\\
2x \le 0
\end{array} \right.
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
\left\{ \begin{array}{l}
x \le - 2\\
x \ge - \frac{1}{2}
\end{array} \right.\\
\left\{ \begin{array}{l}
- 2 < x \le \frac{1}{2}\\
x \ge 1
\end{array} \right.\\
\left\{ \begin{array}{l}
x > \frac{1}{2}\\
x \le 0
\end{array} \right.
\end{array} \right.
\end{array}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 4.40 trang 113 SBT Toán 10
Bài tập 4.41 trang 113 SBT Toán 10
Bài tập 4.43 trang 113 SBT Toán 10
Bài tập 4.44 trang 113 SBT Toán 10
Bài tập 4.45 trang 113 SBT Toán 10
Bài tập 32 trang 126 SGK Toán 10 NC
Bài tập 33 trang 126 SGK Toán 10 NC
Bài tập 34 trang 126 SGK Toán 10 NC
Bài tập 35 trang 126 SGK Toán 10 NC
Bài tập 36 trang 127 SGK Toán 10 NC
Bài tập 37 trang 127 SGK Toán 10 NC
Bài tập 38 trang 127 SGK Toán 10 NC
Bài tập 39 trang 127 SGK Toán 10 NC
-


Giải các bất phương trình sau:
bởi Jacky Duyên
 29/04/2020
29/04/2020
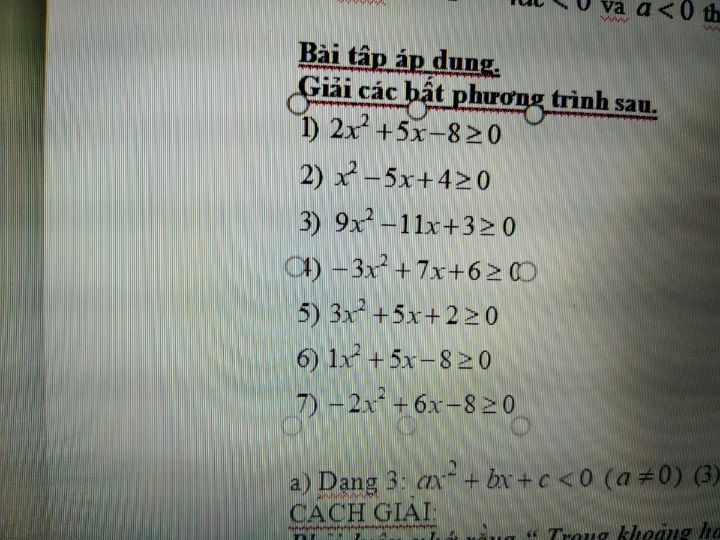 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Lập bảng xét dấu f(x)=3x^2-x-2
bởi Liễu Sam
 28/04/2020
28/04/2020
Lập bảng xét dấu f(x)=3x^2-x-2
Theo dõi (0) 1 Trả lời -


Bât phương trình có tập nghiêm (2; 10)
bởi Nguyễn Hương
 25/04/2020
Bảng xét dấu hộ ạ
25/04/2020
Bảng xét dấu hộ ạ Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -

 1, f(x) =(4x 1).(x-2).(3x 5).(-2x 7)
1, f(x) =(4x 1).(x-2).(3x 5).(-2x 7)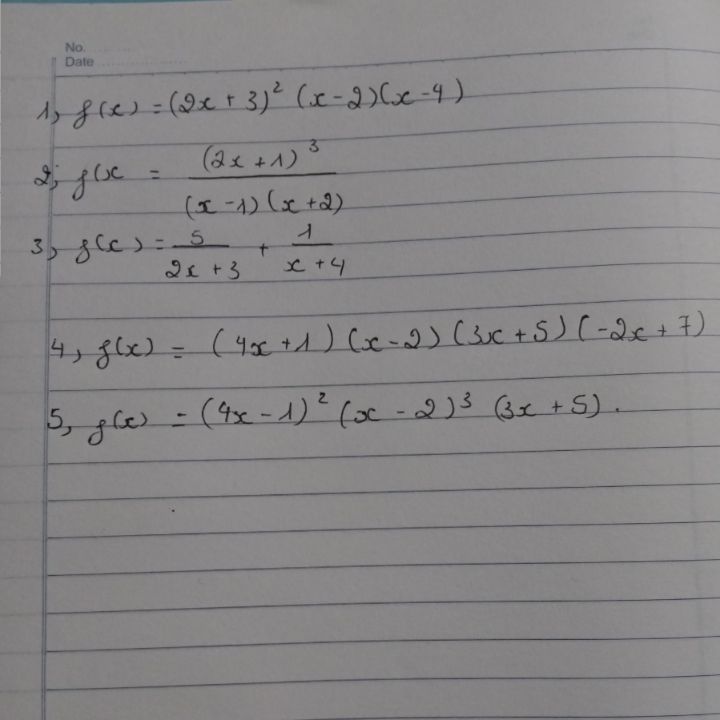 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời