Bài tập 33 trang 126 SGK Toán 10 NC
Phân tích các đa thức sau thành nhân tử bậc nhất rồi xét dấu:
a) \(-x^2+x+6\)
b) \(2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \)
Hướng dẫn giải chi tiết
a) Đặt \(f(x)=-x^2+x+6\)
Ta có \( f(x)=- {x^2} + x + 6 = - \left( {x + 2} \right)\left( {x - 3} \right) = \left( { - x - 2} \right)\left( {x - 3} \right)\)
Bảng xét dấu
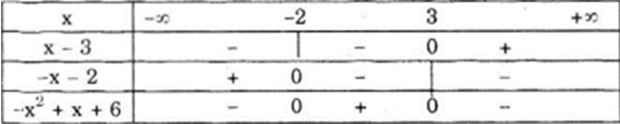
Vậy \(f\left( x \right) < 0\) với \(\left( { - \infty ; - 2} \right) \cup \left( {3; + \infty } \right)\)
\(f\left( x \right) > 0\) với (- 2;3)
\(f(x)=0\) tại x = - 2 và x = 3
b) Đặt \(f(x)=2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 \)
Ta có \(f(x) = 2{x^2} - \left( {2 + \sqrt 3 } \right)x + \sqrt 3 = 2\left( {x - 1} \right)\left( {x - \frac{{\sqrt 3 }}{2}} \right) = \left( {x - 1} \right)\left( {2x - \sqrt 3 } \right)\)
Bảng xét dấu
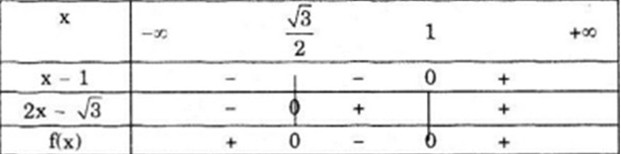
Vậy \(f\left( x \right) < 0\) với \({\left( {\frac{{\sqrt 3 }}{2};1} \right)}\)
\(f\left( x \right) > 0\) với \(\left( { - \infty ;\frac{{\sqrt 3 }}{2}} \right) \cup \left( {1; + \infty } \right)\)
\(f(x)=0\) tại \(x={\frac{{\sqrt 3 }}{2}}\) và x = 1
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 4.45 trang 113 SBT Toán 10
Bài tập 32 trang 126 SGK Toán 10 NC
Bài tập 34 trang 126 SGK Toán 10 NC
Bài tập 35 trang 126 SGK Toán 10 NC
Bài tập 36 trang 127 SGK Toán 10 NC
Bài tập 37 trang 127 SGK Toán 10 NC
Bài tập 38 trang 127 SGK Toán 10 NC
Bài tập 39 trang 127 SGK Toán 10 NC
-


Giải bất phương trình |x-2| < x/2
bởi Linh Lưu
 11/02/2020
11/02/2020
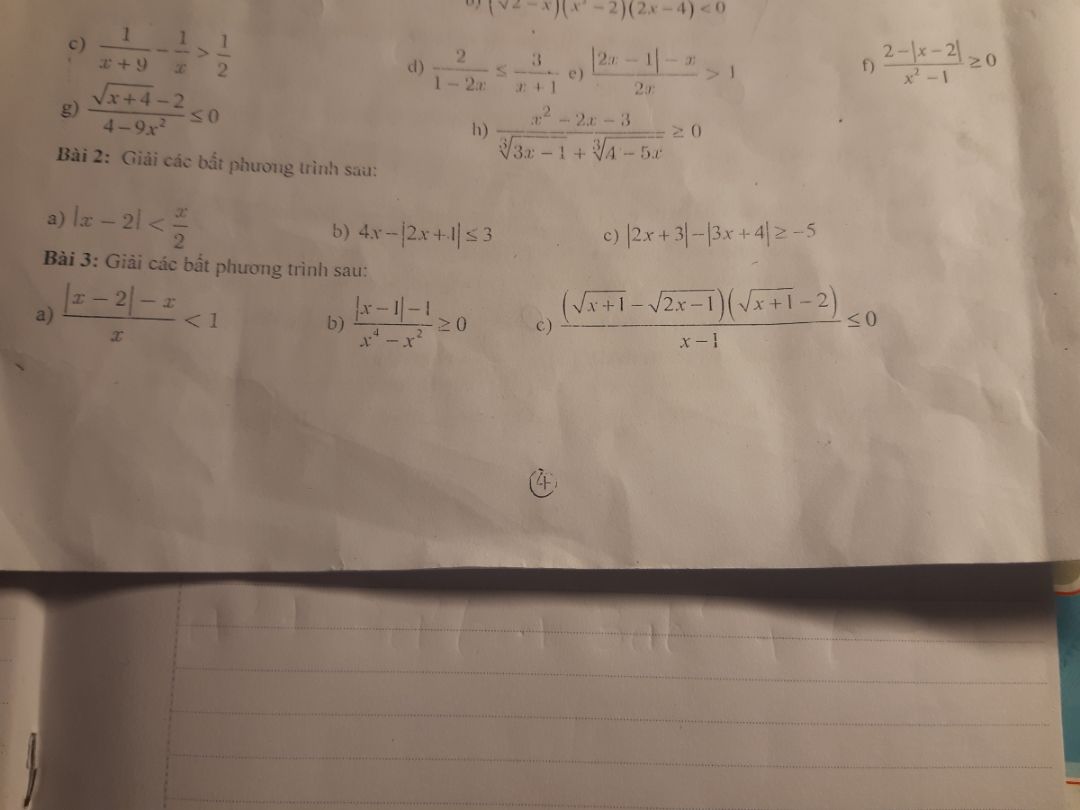 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Giải bất phương trình 1/(x+2) < 1/(x-2)^2
bởi Trần Giang
 07/02/2020
1/x 2< 1/(x-2)^2Theo dõi (0) 0 Trả lời
07/02/2020
1/x 2< 1/(x-2)^2Theo dõi (0) 0 Trả lời -


Nhị thức -2x-3 nhận giá trị dương khi nào?
bởi Phạm Thùy Linh
 07/02/2020
Nhị thức -2x-3 nhận giá trị dương khi nàoTheo dõi (0) 1 Trả lời
07/02/2020
Nhị thức -2x-3 nhận giá trị dương khi nàoTheo dõi (0) 1 Trả lời -

 ..
.. Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời






