Bài tập 41 trang 127 SGK Toán 10 NC
Giải và biện luận bất phương trình
a) \(\left\{ \begin{array}{l}
\left( {x - \sqrt 5 } \right)\left( {\sqrt 7 - 2x} \right) > 0\,(1)\\
x - m \le 0\,\,\,(2)
\end{array} \right.\)
b) \(\left\{ \begin{array}{l}
\frac{2}{{x - 1}} < \frac{5}{{2x - 1}}\,(1)\\
x - m \ge 0\,\,\,(2)
\end{array} \right.\)
Hướng dẫn giải chi tiết
a) Giải (1):
Bảng xét dấu
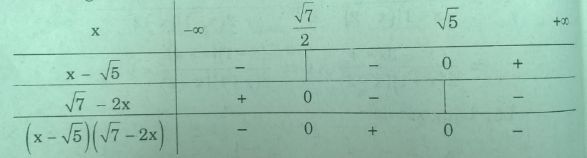
Suy ra \({S_1} = \left( {\frac{{\sqrt 7 }}{2};\sqrt 5 } \right)\)
Ta có \(\left( 2 \right) \Leftrightarrow x \le m\), suy ra \({S_2} = \left( { - \infty ;m} \right]\)
Do đó:
Nếu \(m \le \frac{{\sqrt 7 }}{2}\) thì tập nghiệm là \(S = {S_1} \cap {S_2} = \emptyset \)
Nếu \(\frac{{\sqrt 7 }}{2} \le m < \sqrt 5 \) thì tập nghiệm là \(S = {S_1} \cap {S_2} = \left( {\frac{{\sqrt 7 }}{2};m} \right)\)
Nếu \(m \ge \sqrt 5 \) thfi tập nghiệm là \(S = {S_1} \cap {S_2} = \left( {\frac{{\sqrt 7 }}{5};\sqrt 5 } \right)\)
b)
\(\begin{array}{*{20}{l}}
\begin{array}{l}
\frac{2}{{x - 1}} < \frac{5}{{2x - 1}}\\
\Leftrightarrow \frac{{2\left( {2x - 1} \right) - 5\left( {x - 1} \right)}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} < 0
\end{array}\\
{ \Leftrightarrow \frac{{x - 3}}{{\left( {x - 1} \right)\left( {2x - 1} \right)}} > 0}
\end{array}\)
Bằng cách lập bảng xét dấu, ta có tập nghiệm của (1) là \({S_1} = \left( {\frac{1}{2};1} \right) \cup \left( {3; + \infty } \right)\)
Ta lại có \(\left( 2 \right) \Leftrightarrow x \ge m\), suy ra (2) có tập nghiệm là \({S_2}=\left[ {m; + \infty } \right)\)
Do đó:
Nếu \(x \le \frac{1}{2}\) thì tập nghiệm là \(S = {S_1} \cap {S_2} = \left( {\frac{1}{2};1} \right) \cup \left( {3; + \infty } \right)\)
Nếu \(\frac{1}{2} < m < 1\) thì tập nghiệm là \(S = {S_1} \cap {S_2} = \left[ {m;1} \right) \cup \left( {3; + \infty } \right)\)
Nếu \(1 \le m \le 3\) thì tập nghiệm là \(S = \left( {3; + \infty } \right)\)
Nếu m > 3 thì tập nghiệm là \(S = \left[ {m; + \infty } \right)\)
-- Mod Toán 10 HỌC247
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.





