Bài tập 22 trang 116 SGK Toán 10 NC
Tìm điều kiện xác định rồi suy ra tập nghiệm của mỗi bất phương trình sau:
a) \(\sqrt x > - \sqrt x \)
b) \(\sqrt {x - 3} < 1 + \sqrt {x - 3} \)
c) \(x + \frac{1}{{x - 3}} \ge 2 + \frac{1}{{x - 3}}\)
d) \(\frac{x}{{\sqrt {x - 2} }} < \frac{2}{{\sqrt {x - 2} }}\)
Hướng dẫn giải chi tiết
a) ĐKXĐ: \(\left\{ \begin{array}{l}
x \ge 0\\
- x \ge 0
\end{array} \right. \Leftrightarrow x = 0\)
Ta có x = 0 không là nghiệm của bất phương trình
Vậy \(S = \emptyset \)
b) ĐKXĐ: \(x \ge 3\)
Ta có: \(\sqrt {x - 3} < 1 + \sqrt {x - 3} \Leftrightarrow 0 < 1\) (luôn đúng)
Vậy \(S = \left[ {3; + \infty } \right)\)
c) ĐKXĐ: \(x \ne 3\)
Ta có: \(x + \frac{1}{{x - 3}} \ge 2 + \frac{1}{{x - 3}} \)
\(\Leftrightarrow x \ge 2\)
Vậy \(S = \left[ {2; + \infty } \right)\backslash \left\{ 3 \right\}\)
d) ĐKXĐ: x > 2
Ta có: \(\frac{x}{{\sqrt {x - 2} }} < \frac{2}{{\sqrt {x - 2} }}\)
\(\Leftrightarrow x < 2\) (không thỏa)
Vậy \(S = \emptyset \).
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 4.33 trang 110 SBT Toán 10
Bài tập 21 trang 116 SGK Toán 10 NC
Bài tập 23 trang 116 SGK Toán 10 NC
Bài tập 24 trang 116 SGK Toán 10 NC
Bài tập 25 trang 121 SGK Toán 10 NC
Bài tập 26 trang 121 SGK Toán 10 NC
Bài tập 27 trang 121 SGK Toán 10 NC
Bài tập 28 trang 121 SGK Toán 10 NC
Bài tập 29 trang 121 SGK Toán 10 NC
-


Tìm m để bpt m^2x+4m-3 < x+m^2 vô nghiệm
bởi Hoa Như
 19/01/2020
19/01/2020
Tìm m để các bpt sau vô nghiệm:
a) m2x+4m-3<x+m2
b) m2x+1>= m+(3m-2)x
c) mx-m2>mx-4
d) 3-mx<2.(x-m)-(m+1)2
Theo dõi (0) 5 Trả lời -


Chứng minh các bất phương trình sau vô nghiệm
bởi Thêu Phạm
 08/01/2020
Nhân kiểu j để noa ra như vậy thế ạ
08/01/2020
Nhân kiểu j để noa ra như vậy thế ạ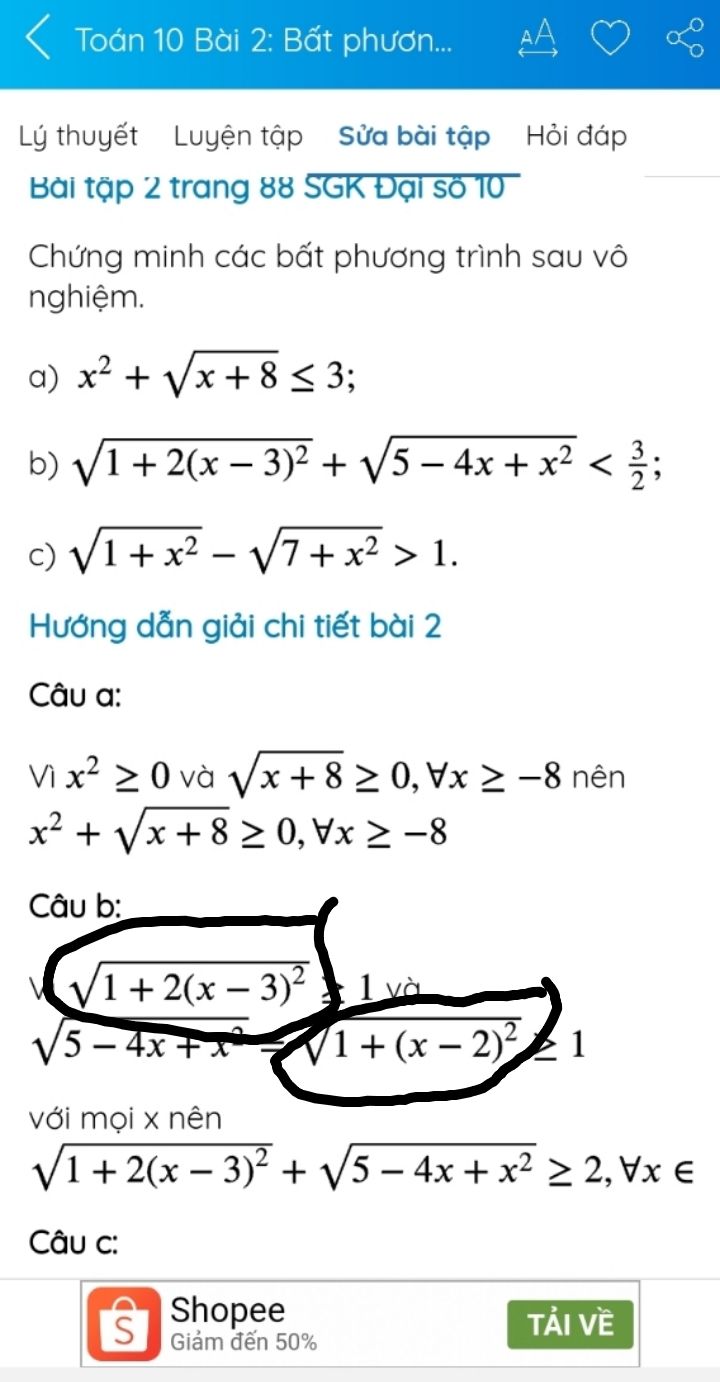 Theo dõi (0) 6 Trả lời
Theo dõi (0) 6 Trả lời -

 Mọi người giúp em với ạ
Mọi người giúp em với ạ Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Tìm m để f(x)=(m+2)x+5-2m > 0 với mọi x thuộc [1;3]
bởi Hiên Hồng
 06/01/2020
06/01/2020
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -
ADMICRO


Chứng minh bất đẳng thức (a^2+b^2+c^2).(1/a+b+1/b+c+1/c+a) > = 3/2(a+b+c)
bởi Dương Nguyễn
 05/01/2020
05/01/2020
Giúp mình giải đề trên nhe mn!
Cảm ơn mọi người nhiều!
Theo dõi (0) 1 Trả lời -


Chứng minh (a+2b).(1/2a+1/b) > = 4
bởi Đào Võ Như Quỳnh
 27/12/2019
Giúp e vs
27/12/2019
Giúp e vs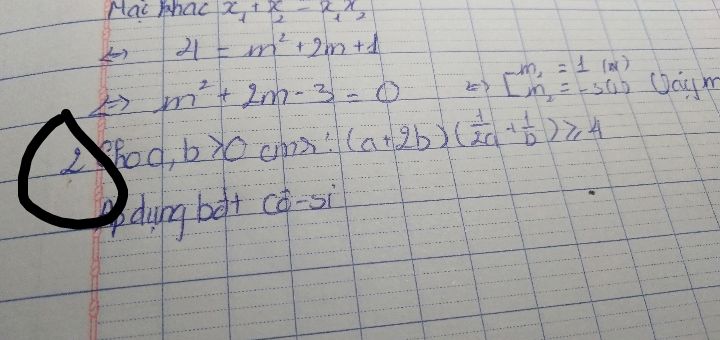 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


Tìm GTLN của biểu thức P=căn(x^2+1)/(x^2+5)
bởi Hải Yến
 17/12/2019
17/12/2019
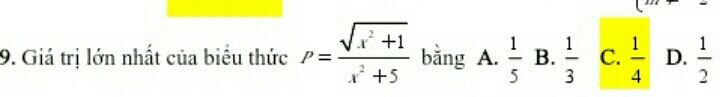 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


- tìm m để bpt sau có nghiệm x2+2|x-m|+m2+m-1<=0
- ai giúp mình vs ạ cần gấp
Theo dõi (1) 0 Trả lời -


Tìm tập nghiệm của bất phương trình (x−a)(ax+b) > 0
bởi Huỳnh Đạt
 28/01/2019
28/01/2019
Mọi người giúp mik với!! Qua tết kt rồi :>>
1. Tìm khẳng định đúng:
A. a<b<=> ac<bc, ∀c>0B. a<b <=> ac<bc
C. a<b <=>
D. a<b <=> ac>bc2. Cho 0<a<b. Tập nghiệm của bất phương trình (x−a)(ax+b)>0 là:
A.
B.
C.
D.
Theo dõi (0) 2 Trả lời





