Giải bài 2.18 tr 41 SBT Đại số 10
Xác định trục đối xứng, tọa độ đỉnh, giao điểm với trục tung và trục hoành của parabol.
a) y = 2x2−x−2;
b) y = −2x2−x+2.
Hướng dẫn giải chi tiết
a) Ta có a = 2; b = −1; c = −2.Ta có Δ = (−1)2−4.2.(−2) = 17.
Trục đối xứng là đường thẳng \(x = \frac{1}{4}\); đỉnh \(I\left( {\frac{1}{4}; - \frac{{17}}{8}} \right)\); giao với trục tung tại điểm (0;−2).
Để tìm giao điểm với trục hoành ta giải phương trình
\(2{x^2} - x - 2 = 0 \Leftrightarrow {x_{1,2}} = \frac{{1 \pm \sqrt {17} }}{4}\)
Vậy các giao điểm với trục hoành là \(\left( {\frac{{1 + \sqrt {17} }}{4};0} \right);\left( {\frac{{1 - \sqrt {17} }}{4};0} \right)\)
b) Ta có a = −2; b = −1; c = 2.Ta có Δ = (−1)2−4.2.(−2)=17.
Trục đối xứng là đường thẳng \(x =- \frac{1}{4}\); đỉnh (I\left( {-\frac{1}{4}; - \frac{{17}}{8}} \right)\); giao với trục tung tại điểm (0;−2).
Để tìm giao điểm với trục hoành ta giải phương trình
\( - 2{x^2} - x + 2 = 0 \Leftrightarrow {x_{1,2}} = \frac{{ - 1 \pm \sqrt {17} }}{4}\)
Vậy các giao điểm với trục hoành là \(\left( {\frac{{ - 1 + \sqrt {17} }}{4};0} \right);\left( {\frac{{ - 1 - \sqrt {17} }}{4};0} \right)\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Bài tập 3 trang 49 SGK Đại số 10
Bài tập 4 trang 50 SGK Đại số 10
Bài tập 2.19 trang 41 SBT Toán 10
Bài tập 2.20 trang 41 SBT Toán 10
Bài tập 2.21 trang 42 SBT Toán 10
Bài tập 2.22 trang 42 SBT Toán 10
Bài tập 2.23 trang 42 SBT Toán 10
Bài tập 2.24 trang 42 SBT Toán 10
Bài tập 2.25 trang 42 SBT Toán 10
Bài tập 2.26 trang 42 SBT Toán 10
Bài tập 27 trang 58 SGK Toán 10 NC
Bài tập 28 trang 59 SGK Toán 10 NC
Bài tập 29 trang 59 SGK Toán 10 NC
Bài tập 30 trang 59 SGK Toán 10 NC
Bài tập 31 trang 59 SGK Toán 10 NC
Bài tập 32 trang 59 SGK Toán 10 NC
Bài tập 33 trang 60 SGK Toán 10 NC
Bài tập 34 trang 60 SGK Toán 10 NC
Bài tập 35 trang 60 SGK Toán 10 NC
Bài tập 36 trang 60 SGK Toán 10 NC
-


Tìm hàm số y=f(x) biết f(2a +4) = a^2 -a +4
bởi Bùi Nhật
 06/09/2020
06/09/2020
tìm hàm số y=f(x) biết f(2a +4) = a^2 -a +4
Theo dõi (0) 0 Trả lời -


Giải các bất phương trình sau?
bởi Nguyễn Tú
 06/06/2020
06/06/2020
Giải đề
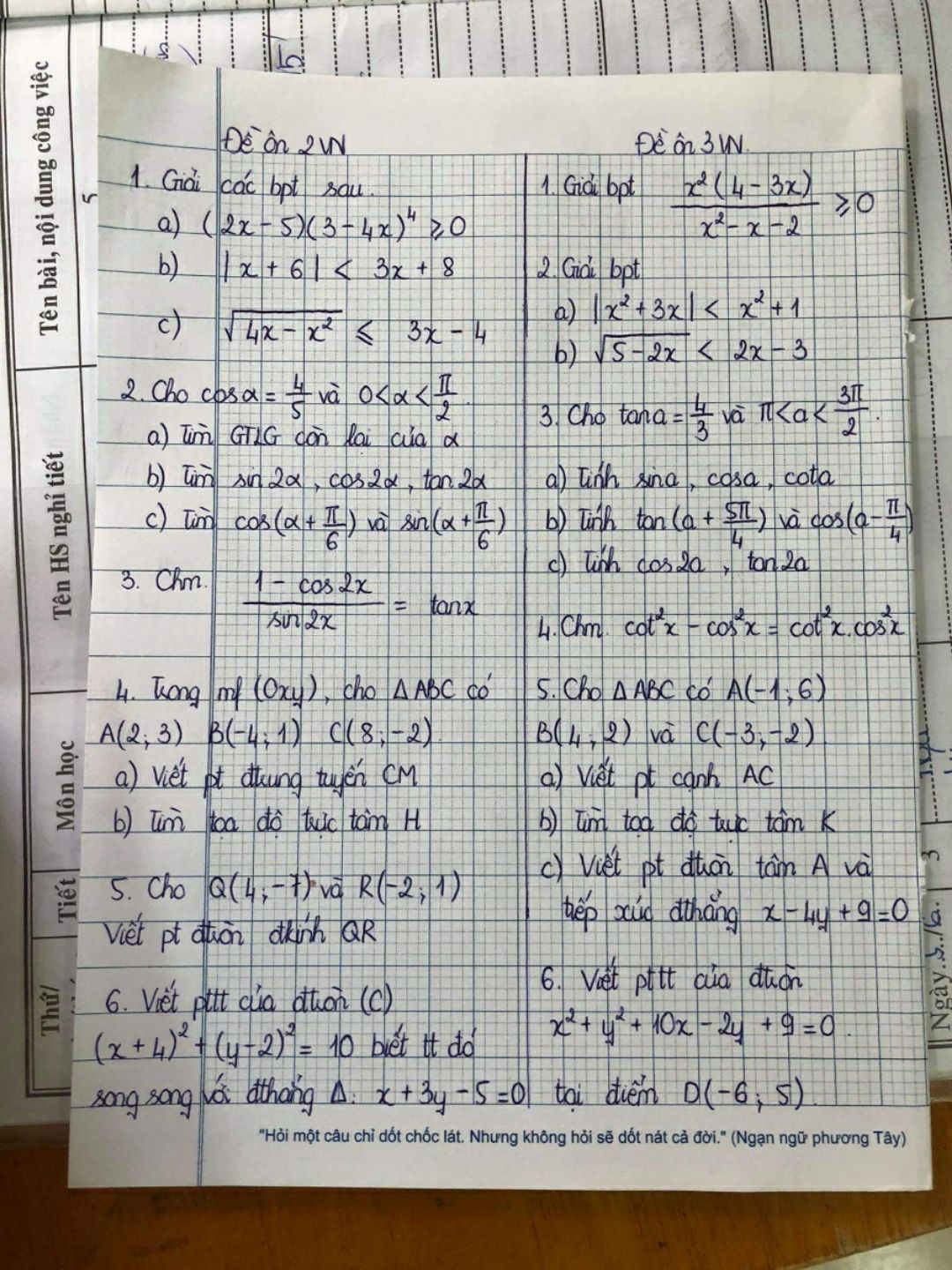 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tìm m để \(y \ge 0,\,\,\,\forall x \in R\)?
bởi Nguyễn Quyên
 01/06/2020
01/06/2020
Giải hộ mik bài 1,2 mik cần gấp
 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Cho parabol (P): y = \({x^2}\) – 2x + m – 1. Tìm tất cả các giá trị thực của tham số m để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương.
bởi Trần Bảo Việt
 25/05/2020
25/05/2020
A. 1 < m < 2.
B. m < 2.
C. m > 2.
D. m < 1.
Theo dõi (0) 1 Trả lời -
ADMICRO


Cho parabol (P): y = \({x^2}\) + x+ 2 và đường thẳng (d): y =ax + 1. Tìm tất cả các giá trị thực của tham số a để (P) tiếp xúc với (d).
bởi Lê Bảo An
 25/05/2020
25/05/2020
A. a = -1; a = 3.
B. a = 2.
C. a = 1; a = -3.
D. Không tồn tại giá trị của a
Theo dõi (0) 1 Trả lời -


Tìm tất cả các giá trị thực của tham số b để đồ thị hàm số y = -3\({x^2}\) + bx – 3 cắt trục hoành tại hai điểm phân biệt.
bởi Lê Bảo An
 25/05/2020
Theo dõi (0) 1 Trả lời
25/05/2020
Theo dõi (0) 1 Trả lời -


Xác định parabol (P): y = a\({x^2}\) + bx + c biết rằng (P) đi qua M(-5; 6) và cắt trục tung tại điểm có tung độ bằng -2. Mệnh đề nào dưới đây đúng?
bởi Trần Bảo Việt
 25/05/2020
25/05/2020
A. a = 6b.
B. 25a – 5b = 8.
C. b = -6a.
D. 25a + 5b = 8.
Theo dõi (0) 1 Trả lời





