Bài tập 32 trang 59 SGK Toán 10 NC
Với mỗi hàm số \(y = -x^2 + 2x + 3\) và \(y = \frac{1}{2}{x^2} + x - 4\), hãy:
a) Vẽ đồ thị của mỗi hàm số.
b) Tìm tập hợp các giá trị x sao cho y > 0.
c) Tìm tập hợp các giá trị x sao cho y < 0.
Hướng dẫn giải chi tiết
a) Tọa độ hàm số: \(y = -x^2 + 2x + 3\)
Tọa độ đỉnh I(1, 4)
Bảng giá trị
Đồ thị hàm số
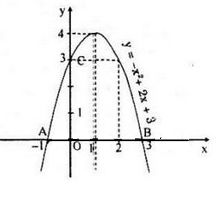
\(y = 0 \Leftrightarrow x = - 1\) hoặc \(x=3\)
\(y > 0 \Leftrightarrow - 1 < x < 3\)
\(y < 0 \Leftrightarrow x < - 1\) hoặc \(x>3\)
b) Đồ thị hàm số \(y = \frac{1}{2}{x^2} + x - 4\)
Tọa độ đỉnh \(I\left( { - 1; - \frac{9}{2}} \right)\)
Bảng giá trị
Đồ thị hàm số
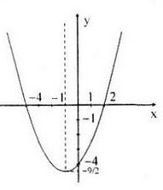
\(\begin{array}{l}
y = 0 \Leftrightarrow \frac{1}{2}{x^2} + x - 4 = 0\\
\Leftrightarrow \left[ {\begin{array}{*{20}{l}}
{x = 2}\\
{x = - 4}
\end{array}} \right.
\end{array}\)
\(y > 0 \Leftrightarrow x < - 4\) hoặc \(x>2\)
\(y < 0 \Leftrightarrow - 4 < x < 2\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
-


Tìm tập xác định của y=căn((x^2+x+2)/(|2x-1|+x-2)
bởi Chai Chai
 22/10/2018
22/10/2018
tìm tập xác định của hàm số y = \(\sqrt {\dfrac{ x^2 + x + 2 } { | 2x - 1 | + x -2 } } \)
Theo dõi (0) 1 Trả lời -


Bài 23 trang 42 sách bài tập Đại số 10
bởi thanh hằng
 06/11/2018
06/11/2018
Bài 23 (SBT trang 42)
Lập bảng biến thiên và vẽ đồ tị của hàm số \(y=x^2-2\left|x\right|+1\)
Theo dõi (0) 1 Trả lời -


Bài 19 trang 41 sách bài tập Toán 10
bởi Mai Hoa
 25/09/2018
Bài 19 (SBT trang 41)
25/09/2018
Bài 19 (SBT trang 41)Một chiếc cổng hình parabl dạng \(y=-\dfrac{1}{2}x^2\) có chiều rộng \(d=8m\). Hãy tính chiều cao h của cổng (h.25) ?
Theo dõi (0) 1 Trả lời -


Bài 18 trang 41 sách bài tập Toán 10
bởi Mai Thuy
 25/09/2018
Bài 18 (SBT trang 41)
25/09/2018
Bài 18 (SBT trang 41)Một chiếc ăng - ten chảo parabol có chiều cao h = 0,5 m và đường kính d = 4m. Ở mặt cắt qua trục ta được một parabol dạng \(y=ax^2\) (h.24)
Hãy xác định hệ số a ?
Theo dõi (0) 1 Trả lời -
ADMICRO


Bài 17 trang 41 sách bài tập Toán 10
bởi cuc trang
 25/09/2018
Bài 17 (SBT trang 41)
25/09/2018
Bài 17 (SBT trang 41)Viết phương trình của parabol \(y=ax^2+bx+c\) ứng với mỗi đồ thị dưới đây ?
Theo dõi (0) 1 Trả lời -


Bài 16 trang 40 sách bài tập Toán 10
bởi Nguyễn Anh Hưng
 25/09/2018
Bài 16 (SBT trang 40)
25/09/2018
Bài 16 (SBT trang 40)Xác định hàm số bậc hai \(y=ax^2-4x+c\), biết rằng đồ thị của nó
a) Đi qua hai điểm \(A\left(1;-2\right);B\left(2;3\right)\)
b) Có đỉnh là \(I\left(-2;-1\right)\)
c) Có hoành độ đỉnh là -3 và đi qua điểm \(P\left(-2;1\right)\)
d) Có trục đối xứng là đường thẳng \(x=2\) và cắt trục hoành tại điểm \(M\left(3;0\right)\)
Theo dõi (0) 1 Trả lời -


Bài 14 trang 40 sách bài tập Toán 10
bởi Nguyen Ngoc
 25/09/2018
Bài 14 (SBT trang 40)
25/09/2018
Bài 14 (SBT trang 40)Xác định trục đối xứng, tọa độ đỉnh, các giao điểm với trục tung và trục hoành của parabol ?
a) \(y=2x^2-x-2\)
b) \(y=-2x^2-x+2\)
c) \(y=-\dfrac{1}{2}x^2+2x-1\)
d) \(y=\dfrac{1}{5}x^2-2x+6\)
Theo dõi (0) 1 Trả lời




.PNG)
.PNG)

