Bài tập 71 trang 116 SBT Toán 9 Tập 1
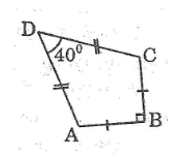
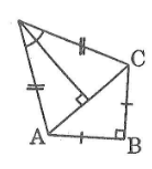
Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, \(\widehat {ADC} = {40^0},\widehat {ABC} = {90^0}\) (hình bên). Hãy tính:
a. Chiều dài cạnh AD.
b. Diện tích của chiếc diều.
Hướng dẫn giải chi tiết
a. Nối AC và kẻ DH ⊥ AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
AC2 = AB2+ BC2 = 122 + 122 = 144 + 144 = 288
Suy ra: AC = 12√2 (cm)
Ta có: ∆ACD cân tại D
DH ⊥ AC
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 69 trang 116 SBT Toán 9 Tập 1
Bài tập 70 trang 116 SBT Toán 9 Tập 1
Bài tập 4.1 trang 116 SBT Toán 9 Tập 1
Bài tập 4.2 trang 116 SBT Toán 9 Tập 1
Bài tập 4.3 trang 117 SBT Toán 9 Tập 1
Bài tập 4.4 trang 117 SBT Toán 9 Tập 1
Bài tập 4.4 trang 117 SBT Toán 9 Tập 1
Bài tập 4.6 trang 117 SBT Toán 9 Tập 1
-


Tính HB, HC, biết AB/AC = 5/7, AH = 15 cm
bởi Nguyễn Thanh Trà
 30/01/2019
30/01/2019
cho tam giác ABC vuông tại A, biết \(\dfrac{AB}{AC}=\dfrac{5}{7}\), ah = 15 cm. Tính HB,,HC
Theo dõi (0) 1 Trả lời -


Tính độ dài AD, có góc A=45, AB=BD=18
bởi Nguyễn Thị Thu Huệ
 30/01/2019
30/01/2019
Bài 1: Cho hình bình hành ABCD có \(\widehat{A}\)=45, AB=BD=18
a) Tính độ dài AD
b) Tính diện tích hbh ABCD
Bài 2: Cho tam giác nhọn ABC, AB<AC, đường cao AH=h và đường trung tuyến AM, đặt \(\widehat{HAM}=\alpha\). CMR:
a) HC - HB =\(2h\tan\alpha\)
b) \(\tan\alpha=\dfrac{\cot C-\cot B}{2}\)
Bài 3: Cho tam giác nhọn ABC. CMR: \(\dfrac{BC}{\sin A}=\dfrac{CA}{\sin B}=\dfrac{AB}{\sin C}\)
Bài 4: Cho tam giác ABC vuông tại A, đường cao AH. Đặt BC=a, CA= b, AB=c. CMR
a)\(AH=a\sin B\cos B\)
b)\(BH=a\cos^2B\)
c)\(CH=a\sin^2B\)
CÁC BẠN GIẢI CHI TIẾT GIÙM MÌNH NHÉ
MÌNH CẢM ƠN Ạ!
Theo dõi (0) 1 Trả lời -


Tính BC, góc B, góc C biết AB=15cm, AC=20cm
bởi Nguyễn Trọng Nhân
 12/02/2019
12/02/2019
Cho tam giác ABC vuông tại A . AB=15cm. AC=20cm
a, Tính BC, \(\widehat{B}\),\(\widehat{C}\)
b, Phân giác góc A cắt BC tại E . Tính BE,CE
c, Từ E kẻ EM và EN vuông với AB và AC . Hỏi tứ giác AMEN là hình gì ?Tính chu vi và diện tích của tứ giác AMEN
d, CM : \(\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{\sqrt{2}}{AE}\)
Theo dõi (0) 1 Trả lời -


Tính các canh AC, BC biết AB=12cm tan B=3/4
bởi Bo Bo
 12/02/2019
12/02/2019
cho tam giác ABC vuông tai A tính các canh AC,BC biết AB=12cm tan B=3/4
Theo dõi (0) 1 Trả lời -
ADMICRO


Chứng minh S_ABCD= 1/2 AC.BD. sin α
bởi Nguyễn Minh Minh
 13/02/2019
13/02/2019
Cho hình chữ nhật ABCD, gọi O là giao điểm 2 đường chéo và góc AOD=\(\alpha\)<90o.
Chứng minh: SABCD=\(\dfrac{1}{2}\)AC.BD.\(\sin\alpha\)
Theo dõi (0) 1 Trả lời