Bài tập 4.8 trang 117 SBT Toán 9 Tập 1
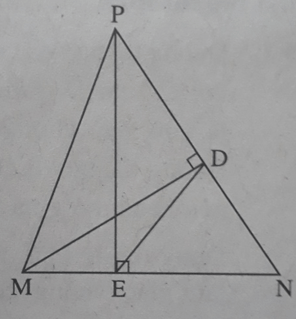
Cho tam giác nhọn MNP. Gọi D là chân đường cao của tam giác đo kẻ từ M. Chứng minh rằng
\(\begin{array}{l}
a){S_{MNP}} = \frac{1}{2}MP.NP.\sin \widehat P\\
b)DP = \frac{{MN.\sin \widehat N}}{{tg\widehat P}}
\end{array}\)
c) ΔDNE ∼ ΔMNP, trong đó E là chân đường cao của tam giác MNP kẻ từ P
Hướng dẫn giải chi tiết
a) Ta có MD = MPsinP, suy ra SMNP = 1/2.NP.MD = 1/2.NP.MP.sinP.
b) Ta có MD = MN.sinN và MD = DP.tgP nên từ đó suy ra
c) Hai tam giác vuông DMN và EPN đồng dạng vì có góc nhọn N chung nên Hai tam giác DNE và MNP đồng dạng vì có góc N chung và
-- Mod Toán 9 HỌC247
-


Tính đường cao trong tam giác thường
bởi Đan Nguyên
 08/09/2017
08/09/2017
các bạn cho mình hỏi một tam giác thường có số đo 3 cạnh rồi thì làm ntn để tính đường cao từ một đỉnh vậy có cách nào tính tổng quát không ?
Bạn nào biết giải mẫu cho mình một bài thử nhen, Ví dụ: Cho tam giác ABC có AB=7,AC=8, BC=9 Tính độ dài đường cao kẻ từ A.
Theo dõi (0) 2 Trả lời