Bài tập 26 trang 67 SBT Toán 9 Tập 1
Cho hai đường thẳng:
y = ax + b (d)
y = a’x + b’ (d’)
Chứng minh rằng: Trên cùng một mặt phẳng tọa độ, hai đường thẳng (d) và (d’) vuông góc với nhau khi và chỉ khi a.a’ = -1
Hướng dẫn giải chi tiết
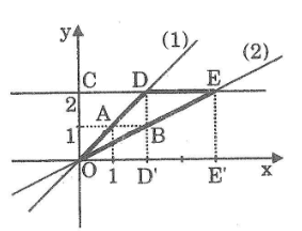
Qua gốc tọa độ, kẻ đường thẳng y = ax // (d) và y = a’x // (d’)
*Chứng minh (d) vuông góc với (d’) thì a.a’ = -1
Không mất tính tổng quát, giả sử a > 0
Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.
Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù (vì các góc tạo bởi đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau 900).
Suy ra: a’ < 0
Mà đường thẳng y = ax đi qua A(1; a), đường thẳng y = a’x đi qua B(1; a’) nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.
Vì (d) ⊥ (d’) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau. Suy ra: góc(AOB) = 900
Tam giác vuông AOB có OH ⊥ AB. Theo hệ thức lượng trong tam giác vuông, ta có: OH2 = HA.HB
Hay: a.|a’| = 1 ⇔ a.(-a’) = 1 ⇔ a.a’ = -1
Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1
*Chứng minh a.a’ = -1 thì (d) vuông góc với (d’)
Ta có: a.a’ = -1 ⇔ a.|a’| = 1 hay HA.HB = OH2
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-
Tìm giá trị của k để ba đường thẳng y = kx – 2; y = 4x + 3; y = (k – 1)x + 4 đồng quy tại một điểm.
bởi Bùi Anh Tuấn
21/01/2021
Theo dõi (0) 1 Trả lời -
Viết phương trình đường thẳng đi qua điểm A(-1;3) và song song với đường thẳng y=2x-3
bởi Nguyễn Linh
29/05/2020
Theo dõi (0) 0 Trả lời -
ADMICRO
Theo dõi (1) 2 Trả lời -
Điểm B(-5;-50) thuộc đồ thị hàm số y=2x^2 không
bởi Châu Bảo
06/05/2020
Theo dõi (0) 1 Trả lời -
ADMICRO
Hỏi điểm B có nằm trên (d) hay không?
bởi Huỳnh Bình
16/04/2020
Theo dõi (0) 0 Trả lời -
Tìm các giá trị sau của m để ba đường thẳng 3x+2y=5, 2x-y=4 và mx+7y=11 đồng quy tại một điểm
bởi Tuyết Lê
11/04/2020
Câu 14
Theo dõi (0) 1 Trả lời -
Tìm m, n để cặp số (-2;-1) là nghiệm của HPT?
bởi Nguyen Phuc
10/04/2020
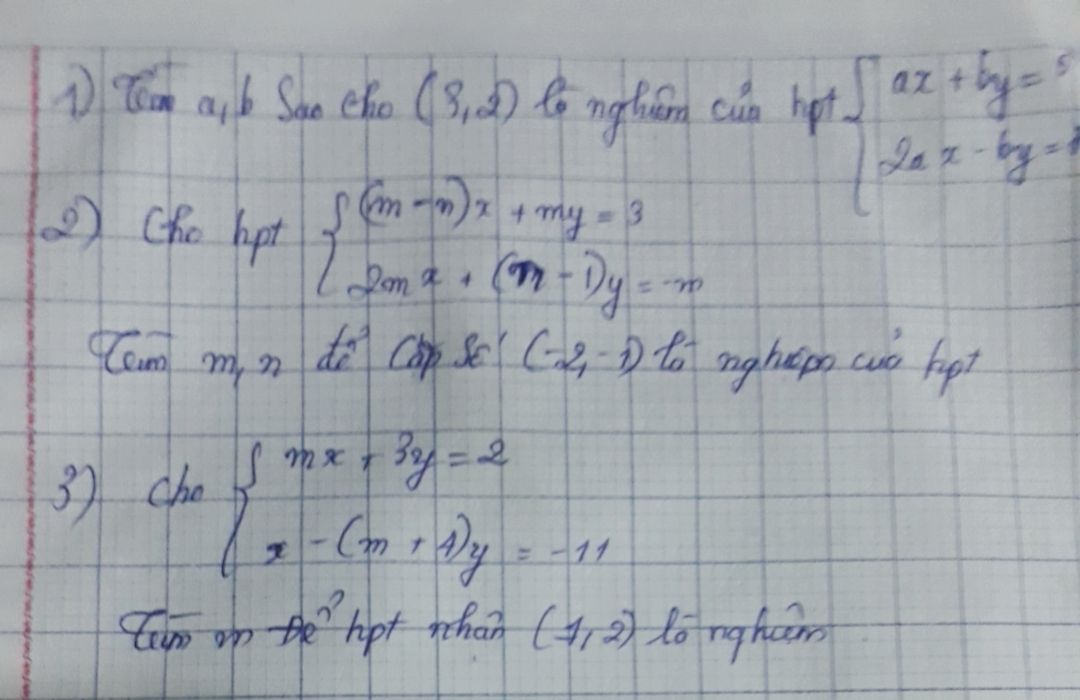Theo dõi (0) 0 Trả lời
