Giải bài 23 tr 53 sách BT Toán lớp 9 Tập 2
Cho phương trình \({1 \over 2}{x^2} - 2x + 1 = 0\)
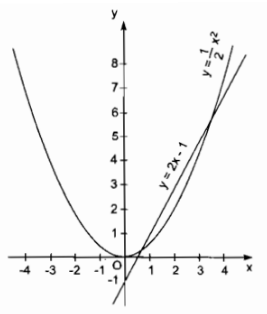
a) Vẽ đồ thị của hàm số \(y = {1 \over 2}{x^2}\) và \(y = 2x - 1\) trên cùng một mặt phẳng tọa độ. Dùng đồ thị tìm giá trị gần đúng nghiệm của phương trình (làm tròn đến chữ số thập phân thứ hai).
b) Giải phương trình đã cho bằng công thức nghiệm, so sánh với kết quả tìm được trong câu a.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Lập bảng giá trị \(x,y\) của hàm số \(\displaystyle y = {1 \over 2}{x^2}\) từ đó vẽ đồ thị của hàm số đó.
- Lấy hai điểm phân biệt thuộc đồ thị hàm số \(y = 2x - 1\), đường thẳng đi qua hai điểm đó là đồ thị của hàm số \(y = 2x - 1\).
* Từ các giao điểm trên đồ thị ta dựng đường thẳng vuông góc với trục hoành cắt trục hoành tại đâu thì đó là hoành độ giao điểm của hai đồ thị đã cho.
Lời giải chi tiết
a) Vẽ đồ thị \(y = {1 \over 2}{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
2 |
| \(y = {1 \over 2}{x^2}\) |
2 |
0 |
2 |
Vẽ đồ thị y = 2x – 1
Cho x = 0 ⇒ y = -1(0; -1)
\({x_1} \approx 0,60;{x_2} \approx 3,40\)
b) \({1 \over 2}{x^2} - 2x + 1 = 0\)
\(\eqalign{
& \Leftrightarrow {x^2} - 4x + 2 = 0 \cr
& \Delta = {\left( { - 4} \right)^2} - 4.1.2 = 16 - 8 = 8 > 0 \cr
& \sqrt \Delta = \sqrt 8 = 2\sqrt 2 \cr
& {x_1} = {{4 + 2\sqrt 2 } \over {2.1}} = 2 + \sqrt 2 \approx 3,41 \cr
& {x_2} = {{4 - 2\sqrt 2 } \over {2.1}} = 2 - \sqrt 2 \approx 0,59 \cr} \)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Tìm m để phương trình \({x^2} + \left( {2m + 1} \right)x + {m^2} = 0\) có nghiệm kép và tính nghiệm kép với m vừa tìm được.
bởi thanh hằng
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(2{x^2} - 5x + 2 = 0\)
bởi Phung Hung
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(16{z^2} + 24z + 9 = 0\)
bởi Sasu ka
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -
ADMICRO


Giải phương trình sau: \({y^2} - 8y + 16 = 0\)
bởi can chu
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(3{x^2} + 5x + 2 = 0\)
bởi hoàng duy
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(6{x^2} + x - 5 = 0\)
bởi sap sua
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(6{x^2} + x + 5 = 0\)
bởi thanh hằng
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình sau: \(2{x^2} - 7x + 3 = 0\)
bởi con cai
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Không giải phương trình, hãy xác định các hệ số \(a, b, c\), tính biệt thức \(∆\) và xác định số nghiệm của phương trình sau: \(1,7{x^2} - 1,2x - 2,1=0\)
bởi Trong Duy
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Không giải phương trình, hãy xác định các hệ số \(a, b, c\), tính biệt thức \(∆\) và xác định số nghiệm của phương trình sau: \(\dfrac{1 }{2}{x^2} + 7x + \dfrac{2 }{3} = 0\)
bởi Mai Vàng
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Không giải phương trình, hãy xác định các hệ số \(a, b, c\), tính biệt thức \(∆\) và xác định số nghiệm của phương trình sau: \(5{x^2} + 2\sqrt {10} x + 2 = 0\)
bởi cuc trang
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Không giải phương trình, hãy xác định các hệ số \(a, b, c\), tính biệt thức \(∆\) và xác định số nghiệm của phương trình sau: \(7{x^2} - 2x + 3 = 0\)
bởi can tu
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(-3x^2+ x + 5 = 0\)
bởi Nguyễn Quang Thanh Tú
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời






