Giải bài 22 tr 53 sách BT Toán lớp 9 Tập 2
Giải phương trình bằng đồ thị.
Cho phương trình \(2{x^2} + x - 3 = 0\)
a) Vẽ các đồ thị của hai hàm số: \(y = 2{x^2},y = - x + 3\) trong cùng một mặt phẳng tọa độ.
b) Tìm hoành độ của mỗi giao điểm của hai đồ thị. Hãy giải thích vì sao các hoành độ này đều là nghiệm của phương trình đã cho.
c) Giải phương trình đã cho công thức nghiệm, so sánh với kết quả tìm được trong câu b.
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Lập bảng giá trị \(x,y\) của hàm số \(y = 2{x^2}\) từ đó vẽ đồ thị của hàm số đó.
- Lấy hai điểm phân biệt thuộc đồ thị hàm số \(y = - x + 3\), đường thẳng đi qua hai điểm đó là đồ thị của hàm số \(y = - x + 3\).
Lời giải chi tiết
a) Vẽ đồ thị hàm số \(y = 2{x^2}\)
|
x |
-2 |
-1 |
0 |
1 |
2 |
| \(y = 2{x^2}\) |
8 |
2 |
0 |
2 |
8 |
Vẽ đồ thị y = -x + 3
Cho x = 0 ⇒ y = 3(0; 3)
Cho y = 0 ⇒ x = 3(3; 0)
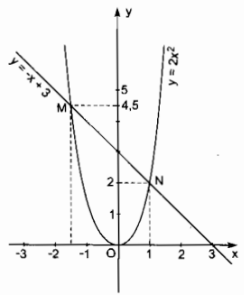
b) M(-1,5; 4,5); N(1; 2)
x = -1,5 là nghiệm của phương trình vì
\(2.{\left( { - 1,5} \right)^2} - 1,5 - 3 = 4,5 - 4,5 = 0\)
x = 1 là nghiệm của phương trình vì
\({2.1^2} + 1 - 3 = 2 + 1 - 3 = 0\)
c) \(2{x^2} + x - 3 = 0\)
\(\eqalign{
& \Delta = {1^2} - 4.2.\left( { - 3} \right) = 1 + 24 = 25 > 0 \cr
& \sqrt \Delta = \sqrt {25} = 5 \cr
& {x_1} = {{ - 1 + 5} \over {2.2}} = {4 \over 4} = 1 \cr
& {x_2} = {{ - 1 - 5} \over {2.2}} = {{ - 6} \over 4} = - 1,5 \cr} \)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 20 trang 53 SBT Toán 9 Tập 2
Bài tập 21 trang 53 SBT Toán 9 Tập 2
Bài tập 23 trang 53 SBT Toán 9 Tập 2
Bài tập 24 trang 54 SBT Toán 9 Tập 2
Bài tập 25 trang 54 SBT Toán 9 Tập 2
Bài tập 26 trang 54 SBT Toán 9 Tập 2
Bài tập 4.1 trang 54 SBT Toán 9 Tập 2
Bài tập 4.2 trang 54 SBT Toán 9 Tập 2
-

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Viết phương trình đường thẳng qua điểm \((0;− 2)\) và tiếp xúc với parabol \(y = 2{x^2}\) (P ).
bởi hành thư
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Tìm m để phương trình \({x^2} - \left( {{m^2} + m} \right)x - 2 = 0\) có nghiệm.
bởi Bao Chau
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Tìm m để parabol \(y = - {x^2}\) (P ) và đường thẳng \(y = x + m\) (d) tiếp xúc nhau.
bởi Thanh Nguyên
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -
ADMICRO


Tìm tọa độ giao điểm của parabol \(y = 2{x^2}\) (P ) và đường thẳng \(y = 5x + 3\) (d).
bởi Lan Ha
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -


Tìm m để phương trình \(m{x^2} + \left( {2m - 1} \right)x + m + 2 = 0\) có nghiệm.
bởi Duy Quang
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để đồ thị hai hàm số \(y = {x^2}\) và \(y = 2mx + 4\) cắt nhau tại hai điểm phân biệt.
bởi Tuyet Anh
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Chứng minh rằng phương trình \({x^2}-ax - 2 = 0\) luôn luôn có hai nghiệm phân biệt với mọi a.
bởi thu hảo
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Tìm m để phương trình \({x^2} - 3x + m = 0\) vô nghiệm.
bởi Hong Van
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời -

 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(2{x^2} + 9x + 7 = 0.\)
bởi Hương Lan
 18/02/2021
Theo dõi (0) 1 Trả lời
18/02/2021
Theo dõi (0) 1 Trả lời -


Giải phương trình: \(2{x^2} - 7x + 2 = 0\)
bởi Mai Đào
 17/02/2021
Theo dõi (0) 1 Trả lời
17/02/2021
Theo dõi (0) 1 Trả lời






