Giải bài 25 tr 54 sách BT Toán lớp 9 Tập 2
Đối với mỗi phương trình sau, hãy tìm các giá trị của m để phương trình có nghiệm; tính nghiệm của phương trình theo m:
a) \(m{x^2} + \left( {2x - 1} \right)x + m + 2 = 0\)
b) \(2{x^2} - \left( {4m + 3} \right)x + 2{m^2} - 1 = 0\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
Phương trình \(a{x^2} + bx + c = 0\) (1) (có chứa tham số \(m\)).
- TH1: \(a=0\) từ đó tìm nghiệm của (1).
- TH2: \(a\ne 0\), phương trình (1) có nghiệm khi và chỉ khi \(\Delta \ge 0\).
Lời giải chi tiết
a) \(m{x^2} + \left( {2m - 1} \right)x + m + 2 = 0\)
Nếu m = 0 ta có phương trình: \( - x + 2 = 0 \Leftrightarrow x = 2\)
Nếu m ≠ 0 phương trình có nghiệm khi và chỉ khi \(\Delta \ge 0\)
\(\eqalign{
& \Delta = {\left( {2m - 1} \right)^2} - 4m\left( {m + 2} \right) \cr
& = 4{m^2} - 4m + 1 - 4{m^2} - 8m \cr
& = - 12m + 1 \cr
& \Delta \ge 0 \Rightarrow - 12m + 1 \ge 0 \Leftrightarrow m \le {1 \over {12}} \cr
& \sqrt \Delta = \sqrt {1 - 12m} \cr
& {x_1} = {{ - \left( {2m - 1} \right) + \sqrt {1 - 12m} } \over {2.m}} = {{1 - 2m + \sqrt {1 - 12m} } \over {2m}} \cr
& {x_2} = {{ - \left( {2m - 1} \right) - \sqrt {1 - 12m} } \over {2.m}} = {{1 - 2m - \sqrt {1 - 12m} } \over {2 + }} \cr} \)
b) \(2{x^2} - \left( {4m + 3} \right)x + 2{m^2} - 1 = 0\)
Phương trình có nghiệm khi và chỉ khi \(\Delta \ge 0\)
\(\eqalign{
& \Delta = {\left[ { - \left( {4m + 3} \right)} \right]^2} - 4.2\left( {2{m^2} - 1} \right) \cr
& = 16{m^2} + 24m + 9 - 16{m^2} + 8 \cr
& = 24m + 17 \cr
& \Delta \ge 0 \Rightarrow 24m + 17 \ge 0 \Leftrightarrow m > - {{17} \over {24}} \cr
& \sqrt \Delta = \sqrt {24m + 17} \cr
& {x_1} = {{4m + 3 + \sqrt {24m + 17} } \over 4} \cr
& {x_2} = {{4m + 3 - \sqrt {24m + 17} } \over 4} \cr} \)
-- Mod Toán 9 HỌC247
Bài tập SGK khác
-


Giải phương trình \(x^2 - 6x + 5=0\)?
bởi Ninh Văn Hoàng
 18/06/2020
18/06/2020
Giải hộ
 Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời -


Tính m + n?
bởi Nguyen Hang
 18/06/2020
18/06/2020
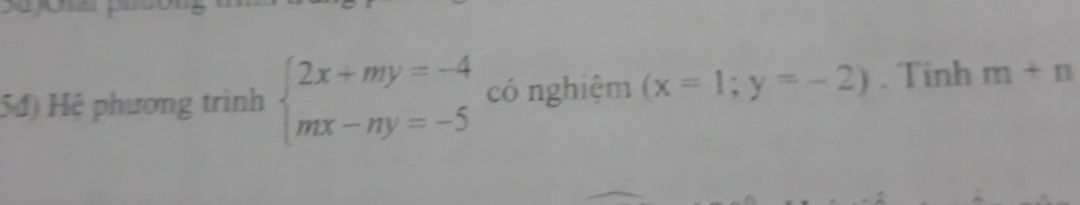 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


 Theo dõi (0) 9 Trả lời
Theo dõi (0) 9 Trả lời -


Giải phương trình \(x^2+18x+17=0\)?
bởi Lê Ngọc Ánh
 14/06/2020
14/06/2020
Giúp e với
Giải phương trình \(x^2+18x+17=0\)?
Theo dõi (0) 0 Trả lời -
ADMICRO


Cho phương trình x^2+2mx-3m^2=0(x là ẩn số). Chứng minh phương trình luôn có nghiệm với mọi giá trị của m. Tính tổng và tích các nghiệm của phương trình theo m.
bởi Nguyễn Hoàng Phương Vy
 24/05/2020
Theo dõi (0) 1 Trả lời
24/05/2020
Theo dõi (0) 1 Trả lời -


Tìm x biết x^2-12x-288=0
bởi Lê Ngọc Ánh
 24/05/2020
Toán lớp 9Theo dõi (0) 2 Trả lời
24/05/2020
Toán lớp 9Theo dõi (0) 2 Trả lời -

 Phương trình : x² 2(m 5)x 10m=0Chứng tỏ phương trình có 2 nghiệm phân biệt .Theo dõi (0) 0 Trả lời
Phương trình : x² 2(m 5)x 10m=0Chứng tỏ phương trình có 2 nghiệm phân biệt .Theo dõi (0) 0 Trả lời -


Tìm các giá trị của m để phương trình vô nghiệm?
bởi Trịnh Thanh Xuân
 17/05/2020
17/05/2020
 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


 Theo dõi (0) 2 Trả lời
Theo dõi (0) 2 Trả lời -


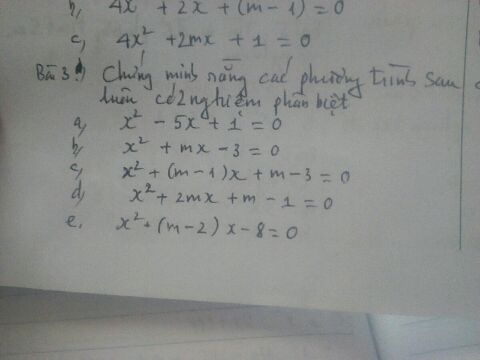 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời -


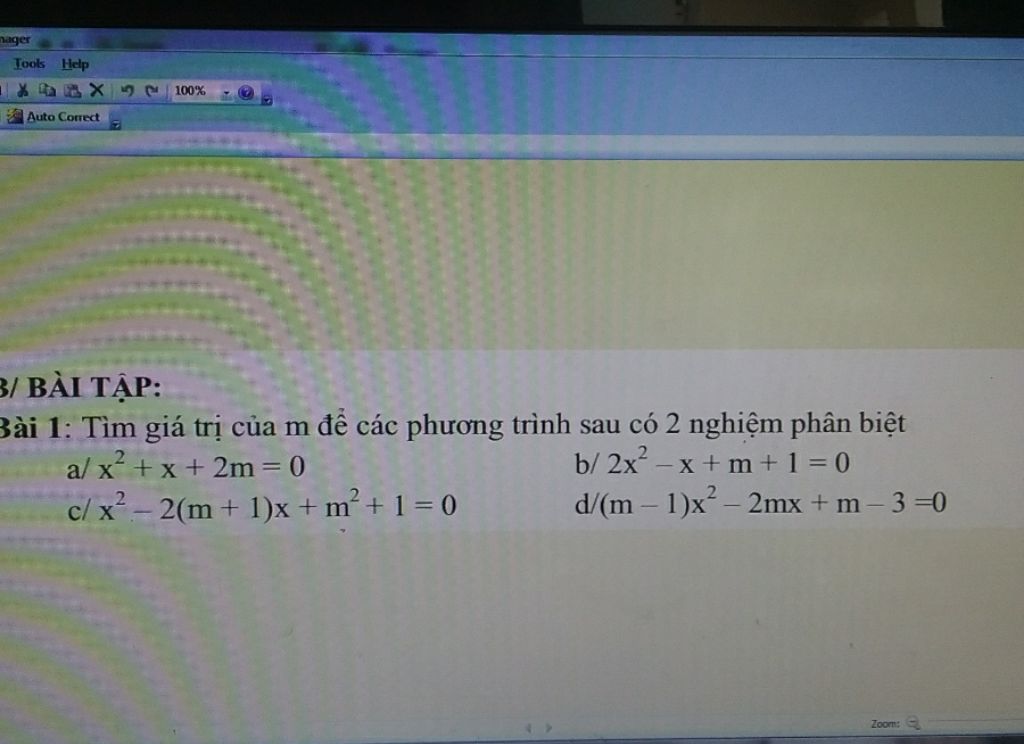 Theo dõi (0) 0 Trả lời
Theo dõi (0) 0 Trả lời -


Giải phương trình 2x^2-5x+1=0
bởi Huỳnh Trâm
 25/04/2020
25/04/2020
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -

 Mình đang cần gấp LÀM ƠN ĐỌC KĨ ĐỀ
Mình đang cần gấp LÀM ƠN ĐỌC KĨ ĐỀ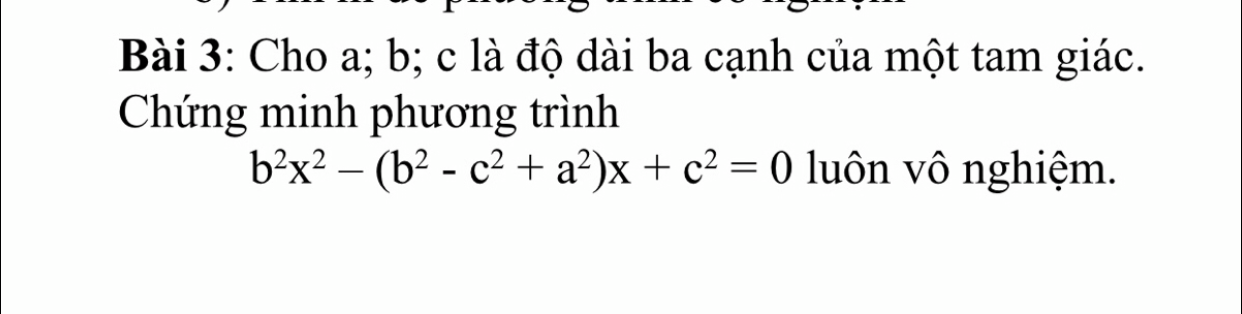 Theo dõi (1) 0 Trả lời
Theo dõi (1) 0 Trả lời -


Xác định các hệ số a, b, c rồi vận dụng công thức tính biệt thức denta của phương trình 2x^2-3x+5=0
bởi Đừng Vội Vàngđổithay
 21/04/2020
21/04/2020
 Theo dõi (1) 2 Trả lời
Theo dõi (1) 2 Trả lời





