Phß║ºn hã░ß╗øng dß║½n giß║úi b├ái tß║¡p To├ín 8 Chã░ãíng 4 B├ái 2 Li├¬n hß╗ç giß╗»a thß╗® tß╗▒ vß╗øi ph├®p nh├ón sß║¢ gi├║p c├íc em nß║»m ─æã░ß╗úc phã░ãíng ph├íp v├á r├¿n luyß╗çn k─® n─âng, giß║úi b├ái tß║¡p tß╗½ SGK ─Éß║íi sß╗æ 8 Tß║¡p 2
-
Bài tập 6 trang 39 SGK Toán 8 Tập 2
Cho a<b. Hãy so sánh
\(2a\) và \(2b\)
\(2a\) và \(a+b\)
\(-a\) và \(-b\)
-
Bài tập 7 trang 40 SGK Toán 8 Tập 2
Sß╗æ a l├á sß╗æ ├óm hay dã░ãíng nß║┐u:
a) \(12a<15a?\)
b) \(4a<3a?\)
c) \(-3a<-5a?\)
-
Bài tập 8 trang 40 SGK Toán 8 Tập 2
Cho a < b, chß╗®ng tß╗Å
a) \(2a-3<2b-3\)
b) \(2a-3<2b+5\)
-
Bài tập 5 trang 39 SGK Toán 8 Tập 2
Mỗi khẳng định sau đúng hay sai? Vì sao?
a) (-6).5 < (-5).5 ;
b) (-6).(-3) < (-5).(-3);
c) (-2003).(-2005) Ôëñ (-2005).2004;
d) -3x2 Ôëñ 0. - VIDEOYOMEDIA
-
Bài tập 10 trang 51 SBT Toán 8 Tập 2
─Éß║Àt dß║Ñu \(ÔÇ£<,\,>,\,ÔëÑ,\,ÔëñÔÇØ\) v├áo chß╗ù chß║Ñm cho th├¡ch hß╗úp :
a) \((-2).3\;...\; (-8).5 \;;\)
b) \(4.(-2)\;...\; (-7).(-2) \;;\)
c) \((-6)^2+2\;...\; 36 + 2\;;\)
d) \(5.(-8)\;...\;135.(-8).\)
-
Bài tập 11 trang 52 SBT Toán 8 Tập 2
Cho \(m < n\), hãy so sánh:
a) \(5m\) và \(5n\)
b) \(-3m\) và \(-3n\)
-
Bài tập 12 trang 52 SBT Toán 8 Tập 2
Sß╗æ \(b\) l├á sß╗æ ├óm, sß╗æ \(0\), hay sß╗æ dã░ãíng nß║┐u:
a) \(5b > 3b\)
b) \(-12b > 8b\)
c) \(-6b  9b\)
d) \(3b Ôëñ 15b\)
-
Bài tập 13 trang 52 SBT Toán 8 Tập 2
Cho \(a<b\), h├úy ─æß║Àt dß║Ñu "\(<,\,>\)" v├áo ├┤ vu├┤ng cho th├¡ch hß╗úp:
a) \(\dfrac{a}{2} \;\square\; \dfrac{b}{2}\) ;
b) \(\dfrac{a}{-3} \;\square\; \dfrac{b}{-3}.\)
-
Bài tập 14 trang 52 SBT Toán 8 Tập 2
Cho \(m > n\), chß╗®ng tß╗Å :
a) \(m + 3 > n + 1\)
b) \(3m + 2 > 3n\)
-
Bài tập 15 trang 52 SBT Toán 8 Tập 2
Cho \(m < n\), chß╗®ng tß╗Å :
a) \(2m + 1 < 2n + 1 ;\)
b) \(4(m ÔÇô 2 ) < 4 (n ÔÇô 2 ) ;\)
c) \(3 ÔÇô 6m > 3 ÔÇô 6n.\)
-
Bài tập 16 trang 52 SBT Toán 8 Tập 2
Cho \(m < n\), chß╗®ng tß╗Å :
a) \(4m + 1 < 4n + 5;\)
b) \(3 ÔÇô 5m > 1 ÔÇô 5n.\)
-
Bài tập 17 trang 52 SBT Toán 8 Tập 2
Cho \(a > 0, \;b > 0\), nß║┐u \(a< b\) h├úy chß╗®ng tß╗Å:
a) \({a^2} < ab\) và \(ab < {b^2}\)
b) \({a^2} < {b^2}\) và \({a^3} < {b^3}\)
-
Bài tập 18 trang 52 SBT Toán 8 Tập 2
Cho \(a > 5\), h├úy cho biß║┐t bß║Ñt ─æß║│ng thß╗®c n├áo xß║úy ra:
a) \(a + 5 > 10\)
b) \(a + 4 > 8\)
c) \(-5 > -a\)
d) \(3a > 13\)
-
Bài tập 19 trang 52 SBT Toán 8 Tập 2
Cho \(a\) l├á sß╗æ bß║Ñt k├¼, h├úy ─æß║Àt dß║Ñu \(<,\,>,\, \le,\,\ge\) v├áo ├┤ vu├┤ng cho ─æ├║ng :
a) \(a^2 \;\square \;0\)
b) \(-a^2 \;\square \;0\)
c) \(a^2 +1\;\square \;0\)
d) \(-a^2-2 \;\square \;0\)
-
Bài tập 20 trang 52 SBT Toán 8 Tập 2
Cho \(a>b\) v├á \(m<n\), h├úy ─æß║Àt dß║Ñu "\(<,>\)" v├áo ├┤ vu├┤ng cho th├¡ch hß╗úp :
a) \(a(m-n) \;\square \; b(m-n);\)
b) \(m(a-b) \;\square \; n(a-b).\)
-
Bài tập 21 trang 52 SBT Toán 8 Tập 2
Cho \(2a > 8\), chß╗®ng tß╗Å \(a > 4.\)
─Éiß╗üu ngã░ß╗úc lß║íi l├á g├¼ ? ─Éiß╗üu ─æ├│ c├│ ─æ├║ng kh├┤ng ?
-
Bài tập 22 trang 52 SBT Toán 8 Tập 2
a. Cho bß║Ñt ─æß║│ng thß╗®c m > 0.
Nhß║¡n cß║ú hai vß║┐ cß╗ºa bß║Ñt ─æß║│ng thß╗®c vß╗øi sß╗æ n├áo th├¼ ─æã░ß╗úc bß║Ñt ─æß║│ng thß╗®c \({1 \over m} > 0\) ?
b. Cho bß║Ñt ─æß║│ng thß╗®c m < 0.
Nh├ón cß║ú hai vß║┐ cß╗ºa bß║Ñt ─æß║│ng thß╗®c vß╗øi sß╗æ n├áo th├¼ ─æã░ß╗úc bß║Ñt ─æß║│ng thß╗®c \({1 \over m} < 0\) ?
-
Bài tập 23 trang 53 SBT Toán 8 Tập 2
Cho \(a > 0,\; b> 0\) v├á \(a > b\). Chß╗®ng tß╗Å \(\dfrac{1}{a} <\dfrac{1}{b}.\)
-
Bài tập 24 trang 53 SBT Toán 8 Tập 2
Điền dấu "\(<,\,>\)" vào ô vuông cho đúng :
a) \((0,6)^2\;\square \; (0,6);\)
b) \((1,3)^2\;\square \; 1,3.\)
-
Bài tập 25 trang 53 SBT Toán 8 Tập 2
So sánh \({m^2}\) và \(m\) nếu:
a) \(m\) lß╗øn hãín \(1;\)
b) \(m\) dã░ãíng nhã░ng nhß╗Å hãín \(1.\)
-
Bài tập 26 trang 53 SBT Toán 8 Tập 2
Cho \(a < b\) v├á \(c < d\), chß╗®ng tß╗Å \(a + c < b + d.\)
-
Bài tập 27 trang 53 SBT Toán 8 Tập 2
Cho a, b, c, d l├á c├íc sß╗æ dã░ãíng thß╗Åa m├ún a < b, c < d, chß╗®ng tß╗Å ac < bd.
-
Bài tập 28 trang 53 SBT Toán 8 Tập 2
Chß╗®ng tß╗Å rß║▒ng vß╗øi \(a\) v├á \(b\) l├á c├íc sß╗æ bß║Ñt k├¼ th├¼ :
a) \({a^2} + {b^2} - 2ab \ge 0\);
b) \(\displaystyle {{{a^2} + {b^2}} \over 2} \ge ab\).
-
Bài tập 29 trang 53 SBT Toán 8 Tập 2
Cho \(a\) v├á \(b\) l├á c├íc sß╗æ dã░ãíng, chß╗®ng tß╗Å :
\(\displaystyle {a \over b} + {b \over a} \ge 2\)
-
Bài tập 30 trang 53 SBT Toán 8 Tập 2
a) Vß╗øi sß╗æ \(a\) bß║Ñt k├¼, chß╗®ng tß╗Å \(a\left( {a + 2} \right) < {\left( {a + 1} \right)^2}.\)
b) Chß╗®ng minh rß║▒ng : Trong ba sß╗æ nguy├¬n li├¬n tiß║┐p th├¼ b├¼nh phã░ãíng sß╗æ ─æß╗®ng giß╗»a lß╗øn hãín t├¡ch hai sß╗æ c├▓n lß║íi.
-
Bài tập 2.1 trang 53 SBT Toán 8 Tập 2
Cho ba số \(a,\, b\) và \(k\) mà \(a > b\). Nếu \(ak < bk\) thì số \(k\) là
A. Sß╗æ dã░ãíng
B. Số \(0\)
C. Số âm
D. Số bất kì.
Khoanh tr├▓n v├áo chß╗» c├íi trã░ß╗øc khß║│ng ─æß╗ïnh ─æ├║ng.
-
Bài tập 2.2 trang 53 SBT Toán 8 Tập 2
Cho hai sß╗æ \(a\) v├á \(b\) m├á \(ÔÇô 7a < -7b\)
Khoanh tr├▓n v├áo chß╗» c├íi trã░ß╗øc khß║│ng ─æß╗ïnh ─æ├║ng trong c├íc khß║│ng ─æß╗ïnh sau:
A. \(a ÔÇô 7 < b - 7\)
B. \(a > b\)
C. \(a < b\)
D. \(a Ôëñ b\)
-
Bài tập 2.3 trang 54 SBT Toán 8 Tập 2
Cho a l├á sß╗æ bß║Ñt k├¼, h├úy ─æß║Àt dß║Ñu ÔÇ£<, >, Ôëñ, ÔëÑÔÇØ v├áo ├┤ vu├┤ng cho ─æ├║ng
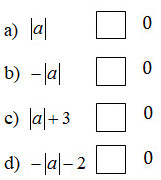
-
Bài tập 2.4 trang 54 SBT Toán 8 Tập 2
─Éß║Àt dß║Ñu "\(<,\,>\)" v├áo ├┤ vu├┤ng cho ─æ├║ng :
a) \(-3\,\square \,-2;\) \((-3)^2 \,\square \, (-2)^2\)
b) \(-2\,\square \,1;\) \((-2)^2 \,\square \, 1^2\)
c) \(2\,\square \,3;\) \(2^2 \,\square \, 3^2\)
d) \(-2\,\square \,2,5;\) \((-2)^2 \,\square \, (2,5)^2\)
-
Bài tập 2.5 trang 54 SBT Toán 8 Tập 2
a) Cho \(\displaystyle x > 0\), chß╗®ng tß╗Å \(\displaystyle x + {1 \over x} \ge 2.\)
b) Từ kết quả câu a, nếu \(x < 0\) sẛ có kết quả nào?


