Giải bài 2.3 tr 54 sách BT Toán lớp 8 Tập 2
Cho a là số bất kì, hãy đặt dấu “<, >, ≤, ≥” vào ô vuông cho đúng
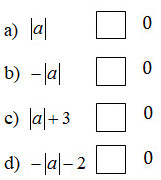
Hướng dẫn giải chi tiết
Hướng dẫn giải
- Áp dụng các tính chất liên hệ giữa thứ tự và phép nhân với số dương và số âm, liên hệ giữa thứ tự và phép cộng.
- Áp dụng tính chất của giá trị tuyệt đối \(\left| a \right| ≥ 0 \) với mọi \(a.\)
Lời giải chi tiết
a) Với \(a=0\) thì \(\left| a \right| = 0 \).
Với \(a\ne0\) thì \(\left| a \right| > 0 \)
Vậy với mọi \(a\) thì \(\left| a \right| ≥ 0 .\)
b) Ta có : \(\left| a \right| ≥ 0 \)
\(\Rightarrow (-1) .\left| a \right| ≤ (-1).0 \) (Nhân số \(-1\) vào hai vế của bất đẳng thức \(\left| a \right| ≥ 0 \)).
Hay \(-\left| a \right| \le 0 .\)
c) - Nếu \(a = 0\), ta có \(\left| a \right| = 0\)
Khi đó \(\left| a \right| + 3 = 3>0,\)
- Nếu \(a ≠ 0\), ta có \(\left| a \right| > 0\) , suy ra \(\left| a \right| + 3 > 3\) \((1)\)
Lại có : \( 3 > 0\) \((2)\)
Từ \((1)\) và \((2)\), theo tính chất bắc cầu ta có \(\left| a \right| + 3 > 0\)
Vậy : \(\left| a \right| + 3 > 0\) với \(a\) bất kì.
d) Theo câu b) ta có : \(-\left| a \right| \le 0 \)
- Nếu \(a = 0\), ta có \(\left| a \right| = 0\)
Khi đó \(-\left| a \right| - 2 = -2<0.\)
- Nếu \(a ≠ 0\), ta có \(\left| a \right| > 0\) , suy ra \(-\left| a \right| <0\)
\(\Rightarrow -\left| a \right| + (-2 )< 0+(-2 ) \)
\(\Rightarrow -\left| a \right| -2 < -2 \) \((3)\)
Lại có : \( -2 < 0\) \((4)\)
Từ \((3)\) và \((4)\), theo tính chất bắc cầu ta có \(-\left| a \right| -2 < 0.\)
Vậy : \(-\left| a \right| -2< 0\) với \(a\) bất kì.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Bài 25 trang 53 sách bài tập toán 8 tập 2
bởi Cam Ngan
 13/10/2018
Bài 25 (Sách bài tập - tập 2 - trang 53)
13/10/2018
Bài 25 (Sách bài tập - tập 2 - trang 53)So sánh \(m^2\) và \(m\) nếu :
a) \(m>1\)
b) \(m\) dương nhưng nhỏ hơn 1
Theo dõi (0) 3 Trả lời -


Bài 24 trang 53 sách bài tập toán 8 tập 2
bởi Bi do
 13/10/2018
Bài 24 (Sách bài tập - tập 2 - trang 53)
13/10/2018
Bài 24 (Sách bài tập - tập 2 - trang 53)Điền dấu " <, >" vào chỗ trống cho đúng :
a) \(\left(0,6\right)^2........\left(0,6\right)\)
b) \(\left(1,3\right)^2.........1,3\)
Theo dõi (0) 2 Trả lời -


Bài 23 trang 53 sách bài tập toán 8 tập 2
bởi Co Nan
 26/12/2018
26/12/2018
Bài 23 (Sách bài tập - tập 2 - trang 53)
Cho \(a>0,b>0\), chứng tỏ \(\dfrac{1}{a}< \dfrac{1}{b}\)
Theo dõi (0) 1 Trả lời -


Bài 22 trang 52 sách bài tập toán 8 tập 2
bởi Bin Nguyễn
 26/12/2018
26/12/2018
Bài 22 (Sách bài tập - tập 2 - trang 52)
a) Cho bất đẳng thức \(m>0\)
Nhân cả hai vế của bất đẳng thức với số nào thì được bất đẳng thức \(\dfrac{1}{m}>0\) ?
b) Cho bất đẳng thức \(m< 0\)
Nhân cả hai vế của bất đẳng thức với số nào thì được bất đẳng thức \(\dfrac{1}{m}< 0\) ?
Theo dõi (0) 1 Trả lời -
ADMICRO


Bài 21 trang 52 sách bài tập toán 8 tập 2
bởi thanh duy
 13/10/2018
Bài 21 (Sách bài tập - tập 2 - trang 52)
13/10/2018
Bài 21 (Sách bài tập - tập 2 - trang 52)Cho \(2a>8\), chứng tỏ \(a>4\)
Điều ngược lại là gì ? Điều đó có đúng không ?
Theo dõi (0) 1 Trả lời -


Bài 18 trang 52 sách bài tập toán 8 tập 2
bởi Nguyễn Hiền
 13/10/2018
Bài 18 (Sách bài tập - tập 2 - trang 52)
13/10/2018
Bài 18 (Sách bài tập - tập 2 - trang 52)Cho \(a>5\), hãy cho biết bất đẳng thức nào xảy ra :
a) \(a+5>10\)
b) \(a+4>8\)
c) \(-5>-a\)
d) \(3a>13\)
Theo dõi (0) 2 Trả lời -


Bài 17 trang 52 sách bài tập toán 8 tập 2
bởi Bánh Mì
 13/10/2018
Bài 17 (Sách bài tập - tập 2 - trang 52)
13/10/2018
Bài 17 (Sách bài tập - tập 2 - trang 52)Cho \(a>0,b>0\), nếu \(a< b\) hãy chứng tỏ :
a) \(a^2< ab\) và \(ab< b^2\)
b) \(a^2< b^2\) và \(a^3< b^3\)
Theo dõi (0) 1 Trả lời





