Giải bài tập Toán 8 Chân trời sáng tạo Chương 8 Bài 1: Hai tam giác đồng dạng

Hai tam giác có ba cạnh bằng nhau thì bằng nhau. Còn hai tam giác có ba góc bằng nhau thì có bằng nhau không?

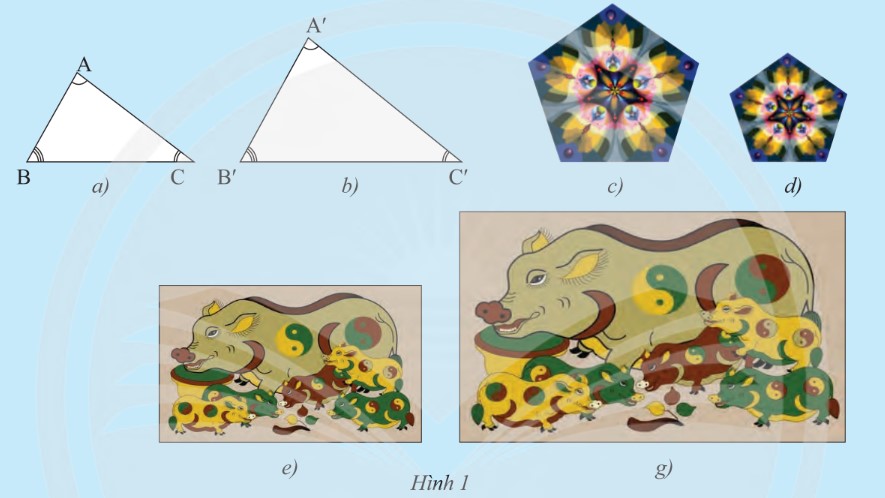
Nêu nhận xét về hình dạng và kích thước của từng cặp hình: Hình 1a và Hình 1b, Hình 1c và Hình 1d, Hình 1e và Hình 1g?

Cho tam giác \(ABC\) và tam giác \(A'B'C'\) như Hình 2:

a) Hãy viết các cặp góc bằng nhau?

b) Tính và so sánh các tỉ số \(\frac{A'B'}{AB};\frac{A'C'}{AC};\frac{B'C'}{BC}\)

Quan sát Hình 3, cho biết \(\Delta AMNᔕ\Delta ABC\)

a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng?

b) Tính \(\widehat{AMN}\)?

a) Nếu \(\Delta A'B'C'=\Delta ABC\) thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Tỉ số đồng dạng là bao nhiêu?

b) Cho \(\Delta A'B'C' ᔕ\Delta ABC\) theo tỉ số k thì \(\Delta ABC ᔕ\Delta A'B'C'\) theo tỉ số nào?

Quan sát Hình 4, cho biết \(\Delta ADEᔕ \Delta AMN,\Delta AMNᔕ \Delta ABC\), DE là đường trung bình của tam giác AMN, MN là đường trung bình của tam giác ABC. Tam giác ADE đồng dạng tam giác ABC theo tỉ số đồng dạng là bao nhiêu?

Quan sát Hình 5, biết \(MN // BC\). Hãy điền vào ? cho thích hợp

\(\Delta AMN\) và \(\Delta ABC\)

\(\widehat{A}\) chung

\(\widehat{M}=?\)

\(\widehat{N}=?\)

\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{?}{?}\)

Nêu nhận xét về mối quan hệ giữa tam giác AMN và tam giác ABC?

Quan sát Hình 8, cho biết \(DC // MP, EF // MQ\):

a) Chứng minh rằng \(\Delta EPFᔕ\Delta DCQ\)?

b) \(\Delta ICF\) có đồng dạng \(\Delta MPQ\) không? Tại sao?

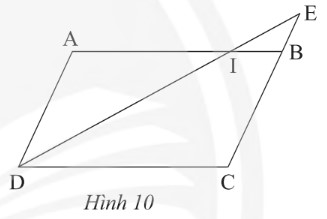
Trong Hình 10, cho biết \(ABCD\) là hình bình hành

a) Chứng minh rằng \(\Delta IEBᔕ\Delta IDA\)?

b) Cho biết \(CB = 3BE\) và \(AI = 9~cm\). Tính độ dài DC?

Trong hai khẳng định sau, khẳng định nào đúng, khẳng định nào sai? Tại sao?

a) Hai tam giác bằng nhau thì đồng dạng với nhau?

b) Hai tam giác đồng dạng với nhau thì bằng nhau?

Cho tam giác ABC, hãy vẽ một tam giác đồng dạng với tam giác ABC theo tỉ số đồng dạng \(k=\frac{1}{2}\)?

a) Trong Hình 11, cho biết \(\Delta ABCᔕ\Delta A'B'C'\). Viết tỉ số đồng dạng của các cạnh tương ứng và chỉ ra các cặp góc tương ứng?

b) Trong Hình 12, cho biết \(\Delta DEFᔕ\Delta D'E'F'\). Tính số đo \(\widehat{D'}\) và \(\widehat{F'}\)?

c) Trong Hình 13, cho biết \(\Delta MNPᔕ\Delta M'N'P'\). Tính độ dài các đoạn thẳng MN và M'P'?

Trong Hình 14, cho biết \(AB // CD\).

a) Chứng minh rằng ΔAEB ᔕ ΔDEC?

b) Tìm x?

Cho \(\Delta ABCᔕ\Delta DEF\) theo tỉ số đồng dạng \(k=\frac{2}{5}\).

a) Tính tỉ số chu vi của hai tam giác đã cho?

b) Cho biết hiệu chu vi của hai tam giác trên là 36 cm, tính chu vi của mỗi tam giác?

Người ta ứng dụng hai tam giác đồng dạng để đo khoảng cách BC ở hai địa điểm không thể đến được (Hình 15). Biết DE // BC

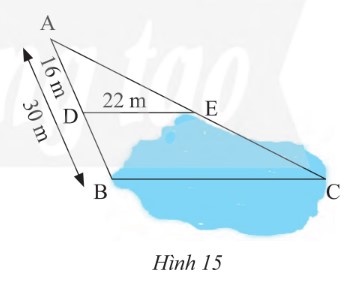
a) Chứng minh rằng \(\Delta ADEᔕ\Delta ABC\)?

b) Tính khoảng cách BC?