Vận dụng trang 65 SGK Toán 8 Chân trời sáng tạo Tập 2
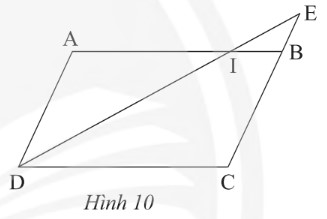
Trong Hình 10, cho biết \(ABCD\) là hình bình hành
a) Chứng minh rằng \(\Delta IEBᔕ\Delta IDA\)?
b) Cho biết \(CB = 3BE\) và \(AI = 9~cm\). Tính độ dài DC?
Hướng dẫn giải chi tiết Vận dụng
a) Ta có: ABCD là hình bình hành suy ra BE // AD
Do đó \(\Delta IEBᔕ\Delta IDA\)
b) \(\Delta IEBᔕ\Delta IDA\) suy ra \(\frac{IB}{IA}=\frac{IE}{ID}\)
Ta có: IB // CD nên \(\Delta IEBᔕ\Delta DEC\)
Do đó \(\frac{IB}{DC}=\frac{IE}{DE}=\frac{EB}{EC}=\frac{1}{4}\) nên \(\frac{IE}{ID}=\frac{1}{3}\)
Suy ra \(\frac{IB}{IA}=\frac{1}{3}\Rightarrow IB=3 \Rightarrow AB = IA + IB = 12\)
Ta có: \(DC = AB = 12~cm\)
Vậy \(DC = 12~cm\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Khám phá 4 trang 64 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Thực hành 3 trang 65 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 1 trang 65 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 2 trang 65 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 3 trang 65 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 4 trang 66 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 5 trang 66 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Bài tập 6 trang 66 SGK Toán 8 Chân trời sáng tạo Tập 2 - CTST
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.


