Nếu các em có gặp khó khăn nào về bài Hình học 8 Bài 3 Diện tích tam giác, các em vui lòng đặt câu hỏi để được giải đáp. Các em có thể đặt câu hỏi ở trong phần bài tập SGK, bài tập nâng cao, cộng đồng Toán HOC247 sẽ sớm giải đáp cho các em.
-
Bài tập 16 trang 121 SGK Toán 8 Tập 1
Giải thích vì sao diện tích của tam giác được tô đậm trong các hình 128,129, 130 bằng nửa diện tích hình chữ nhật tương ứng:
.png)
-
Bài tập 17 trang 121 SGK Toán 8 Tập 1
Cho tam giác AOB vuông tại O với đường cao OM (h.131). Hãy giải thích vì sao ta có đẳng thức: AB. OM = OA. OB.
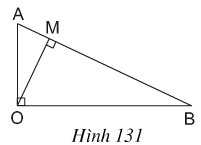
-
Bài tập 18 trang 121 SGK Toán 8 Tập 1
Cho tam giác ABC và đường trung tuyến AM(h. 132). Chứng minh rằng: SAMB = SAMC
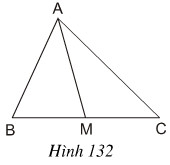
-
Bài tập 19 trang 122 SGK Toán 8 Tập 1
a) Xem hình 133. hãy chỉ ra các tam giác có cùng diện tích (lấy ô vuông làm đơn vị diện tích):
b) Hai tam giác có diện tích bằng nhau thì có bằng nhau hay không?
- VIDEOYOMEDIA
-
Bài tập 20 trang 122 SGK Toán 8 Tập 1
Vẽ hình chữ nhật có một cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.
-
Bài tập 21 trang 122 SGK Toán 8 Tập 1
Tính x sao cho diện tích hình chữ nhật ABCD gấp 3 lần diện tích tam giác ADE (h.134)
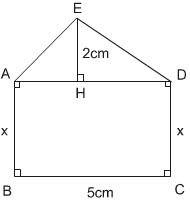
-
Bài tập 22 trang 122 SGK Toán 8 Tập 1
Tam giác PAF được vẽ trên giấy kẻ ô vuông (h.135).
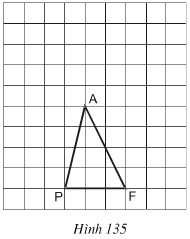
Hãy chỉ ra:
a) Một điểm I sao cho SPIF = SPAF
b) Một điểm O sao cho SPOF = 2. SPAF
c) Một điểm N sao cho SPNF = 1/2 SPAF
-
Bài tập 23 trang 123 SGK Toán 8 Tập 1
Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho: SMAC = SAMB + SBMC
-
Bài tập 24 trang 123 SGK Toán 8 Tập 1
Tính diện tích tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
-
Bài tập 25 trang 123 SGK Toán 8 Tập 1
Tính diện tích của một tam giác đều có cạnh là a.
-
Bài tập 25 trang 159 SBT Toán 8 Tập 1
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?
-
Bài tập 26 trang 159 SBT Toán 8 Tập 1
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên đường thẳng d cố định song song với BC. Chứng minh rằng tam giác ABC có diện tích không đổi.
-
Bài tập 27 trang 159 SBT Toán 8 Tập 1
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A đến đường thẳng BC.
a) Điền vào ô trống bảng sau:
Độ dài AH(cm) 1 2 3 4 5 10 15 20 SABC (cm2) b) Vẽ đồ thị biểu diễn số đo SABC theo độ dài AH.
c) Diện tích tam giác tỉ lệ thuận với chiều cao AH không?
-
Bài tập 28 trang 160 SBT Toán 8 Tập 1
Tính diện tích hình bên theo kích thước đã cho trên hình.
-
Bài tập 29 trang 160 SBT Toán 8 Tập 1
Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:
a) 10 cm2
b). 15 cm2
c) 20 cm2
-
Bài tập 30 trang 160 SBT Toán 8 Tập 1
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ đỉnh B và C.
-
Bài tập 31 trang 160 SBT Toán 8 Tập 1
Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD có độ dài bằng 6cm thành ba đoạn thắng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL. Tính diện tích của ngũ giác AEPSN và của tứ giác PQR
-
Bài tập 32 trang 160 SBT Toán 8 Tập 1
a) Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.
b) Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.
c) Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó.
-
Bài tập 3.2 trang 161 SBT Toán 8 Tập 1
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
-
Bài tập 3.3 trang 161 SBT Toán 8 Tập 1
a) Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC
Chứng minh rằng \(\frac{{S'}}{S} = \frac{{DK}}{{AH}}\)
b) Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T.
Chứng minh rằng \(\frac{{MH}}{{AD}} = \frac{{MK}}{{BE}} + \frac{{MT}}{{CF}} = 1\)
-
Bài tập 25 trang 159 SBT Toán 8 Tập 1
Hai đường chéo của hình chữ nhật chia hình chữ nhật thành bốn tam giác. Diện tích của các tam giác đó có bằng nhau không? Vì sao?
-
Bài tập 26 trang 159 SBT Toán 8 Tập 1
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi.
-
Bài tập 27 trang 159 SBT Toán 8 Tập 1
Tam giác ABC có đáy BC cố định và dài 4cm. Đỉnh A di chuyển trên đường thẳng d (d ⊥ BC). Gọi H là chân đường cao hạ từ đỉnh A xuống đường thẳng BC.
a. Điền vào ô trống trong bảng sau:
Độ dài AH (cm)
1
2
3
4
5
10
15
20
\({S_{ABC}}\)\(\left( {c{m^2}} \right)\)
b. Vẽ đồ thị biểu diễn số đo \({S_{ABC}}\) theo độ dài AH
c. Diện tích tam giác ABC có tỉ lệ thuận với chiều cao AH không ?
-
Bài tập 28 trang 160 SBT Toán 8 Tập 1
Tính diện tích của hình 186 theo các kích thước đã cho trên hình (\(a, b, c\) có cùng đơn vị đo).
-
Bài tập 29 trang 160 SBT Toán 8 Tập 1
Hai cạnh của một tam giác có độ dài là 5cm và 6cm. Hỏi diện tích của tam giác đó có thể lấy giá trị nào trong các giá trị sau:
a. 10 \(c{m^2}\)
b. 15 \(c{m^2}\)
c. 20 \(c{m^2}\)
-
Bài tập 30 trang 160 SBT Toán 8 Tập 1
Cho tam giác ABC, biết AB = 3AC. Tính tỉ số hai đường cao xuất phát từ các đỉnh B và C.
-
Bài tập 31 trang 160 SBT Toán 8 Tập 1
Các điểm E, F, G, H, K, L, M, N chia mỗi cạnh hình vuông ABCD thành ba đoạn thẳng bằng nhau. Gọi P, Q, R, S là giao điểm của EH và NK với FM và GL (h.187). Tính diện tích của ngũ giác AEPSN và của tứ giác PQRS, biết AB = 6cm.
-
Bài tập 3.1 trang 160 SBT Toán 8 Tập 1
a. Có thể dùng kéo cắt hai lần và chỉ cắt theo đường thẳng chia một tam giác (thường) thành ba mảnh để ghép lại được một hình chữ nhật hay không ?
Từ đó suy ra công thức tính diện tích tam giác thường dựa vào công thức tính diện tích hình chữ nhật.
b. Hãy chia một tam giác thành 2 phần có diện tích bằng nhau bởi một đường thẳng đi qua đỉnh của tam giác đó.
c. Hãy chia một tam giác thành 4 phần có diện tích bằng nhau bởi ba đường thẳng, trong đó chỉ có một đường đi qua đỉnh của tam giác đó.
-
Bài tập 3.2 trang 161 SBT Toán 8 Tập 1
Cho tam giác đều ABC và điểm M bất kì nằm trong tam giác đó. Đường thẳng đi qua điểm M và vuông góc với BC tại điểm H. Đường thẳng đi qua điểm M và vuông góc với CA tại điểm K. Đường thẳng đi qua điểm M và vuông góc với AB tại điểm T.
-
Bài tập 3.3 trang 161 SBT Toán 8 Tập 1
a. Cho hai tam giác ABC và DBC. Kẻ đường cao AH của tam giác ABC. Kẻ đường cao DK của tam giác DBC. Gọi S là diện tích của tam giác ABC. Gọi S’ là diện tích của tam giác DBC.
Chứng minh rằng \({{S'} \over S} = {{DK} \over {AH}}\)
b. Cho tam giác ABC và điểm M bất kì nằm trong tam giác đó. Kẻ các đường cao của tam giác đó là AD, BE và CF. Đường thẳng đi qua điểm M và song song với AD cắt cạnh BC tại điểm H. Đường thẳng đi qua điểm M và song song với BE cắt cạnh AC tại điểm K. Đường thẳng đi qua điểm M và song song với CF cắt cạnh BA tại điểm T.
Chứng minh rằng \({{MH} \over {AD}} + {{MK} \over {BE}} + {{MT} \over {CF}} = 1\)


