Giải bài 26 tr 159 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC có đáy BC cố định và đỉnh A di động trên một đường thẳng d cố định song song với đường thẳng BC. Chứng minh rằng tam giác ABC luôn có diện tích không đổi.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Áp dụng công thức tính diện tích tam giác: \(S=\dfrac{1}{2}ah\) với \(h;a\) lần lượt là chiều cao và cạnh đáy tương ứng.
Lời giải chi tiết
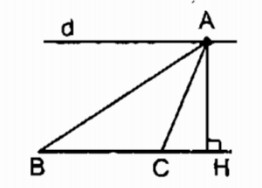
Đường thẳng d cố định song song với đường thẳng BC cố định nên khoảng cách hai đường thẳng d và BC là không đổi.
\(∆ ABC\) có đáy \(BC\) không đổi, chiều cao \(AH\) là khoảng cách giữa hai đường thẳng song song không đổi. Vậy điểm \(A\) thay đổi trên đường thẳng \(d // BC\) thì \({S_{ABC}}=\dfrac {1}{2}AH.BC\) không đổi
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 3.3 trang 161 SBT Toán 8 Tập 1
Bài tập 25 trang 159 SBT Toán 8 Tập 1
Bài tập 27 trang 159 SBT Toán 8 Tập 1
Bài tập 28 trang 160 SBT Toán 8 Tập 1
Bài tập 29 trang 160 SBT Toán 8 Tập 1
Bài tập 30 trang 160 SBT Toán 8 Tập 1
Bài tập 31 trang 160 SBT Toán 8 Tập 1
Bài tập 3.1 trang 160 SBT Toán 8 Tập 1
-


Hình chữ nhật ABCD có chiều dài DC = 27cm, chiều rộng AD = 20,4cm. E là một điểm trên AB. Tính diện tích tam giác ECD?
Theo dõi (0) 1 Trả lời -


Diện tích tam giác
bởi Ha Ku
 25/07/2018
25/07/2018
minh su dung công thuc dien tích tam giác bang nửa cạnh đáy nhân chiều cao thay vì banh nửa tích hai cạnh góc vuông để tính diên tích tam giác vuông có được hay k?
Theo dõi (0) 2 Trả lời -


cho tam giác ABC có diện tích bằng 36( đơn vị diện tích ) . Trên cạnh BC và cạnh AC lấy điểm D và E sao cho DC = 3DB và EA = 2EC ; AD cắt BE tại I . Tính diện tích tam giác BID
Theo dõi (1) 2 Trả lời



