Giải bài 36 tr 87 sách GK Toán 8 Tập 1
Cho góc xOy có số đo 500, điểm A nằm trong góc đó. Vẽ điểm B đối xứng với A qua Ox, vẽ điểm C đối xứng với A qua Oy.
a) So sánh các độ dài OB và OC.
b) Tính số đo góc BOC.
Hướng dẫn giải chi tiết
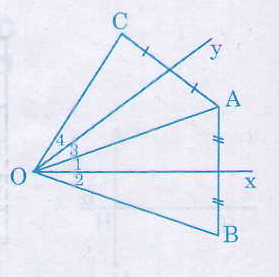
a) Vì \(B\) đối xứng với \(A\) qua \(Ox\) (giả thiết)
\( \Rightarrow Ox\) là đường trung trực của \(AB\)
\( \Rightarrow OA = OB\) (tính chất đường trung trực) (1)
Vì \(C\) đối xứng với \(A\) qua \(Oy\) \( \Rightarrow Oy\) là đường trung trực của \(AC\)
\( \Rightarrow OA = OC\) (tính chất đường trung trực) (2)
Từ (1) và (2) suy ra \( OB = OC.\)
b) Vì \(OA = OB\) (chứng minh trên) \( \Rightarrow ∆AOB\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân).
Trong tam giác cân đường trung trực của cạnh đáy đồng thời là đường phân giác nên \(Ox\) là phân giác của \(\widehat {AOB}\).
\( \Rightarrow \widehat{O_{1}}= \widehat{O_{2}}= \dfrac{1}{2}\widehat{AOB}\)
Lại có \(∆AOC\) cân tại \(O\) (vì \(OA = OC\))
Trong tam giác cân đường trung trực của cạnh đáy đồng thời là đường phân giác nên \(Oy\) là phân giác của \(\widehat {AOC}\).
\( \Rightarrow \widehat{O_{3}}= \widehat{O_{4}}= \dfrac{1}{2}\widehat{AOC}\)
Do đó
\(\widehat{AOB}+\widehat{AOC}=\widehat{O_{1}}+\widehat{O_{2}}+\widehat{O_{3}}+\widehat{O_{4}}\)\(=\widehat{O_{1}}+\widehat{O_{1}}+\widehat{O_{3}}+\widehat{O_{3}}\)\(=2.\widehat{O_{1}}+2.\widehat{O_{3}}= 2(\widehat{O_{1}}+\widehat{O_{3}})\)\(= 2\widehat{xOy}\)\(= {2.50^o}\)\(={100^o}\)
Vậy \(\widehat{BOC}={100^o}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 35 trang 87 SGK Toán 8 Tập 1
Bài tập 37 trang 87 SGK Toán 8 Tập 1
Bài tập 38 trang 88 SGK Toán 8 Tập 1
Bài tập 39 trang 88 SGK Toán 8 Tập 1
Bài tập 40 trang 88 SGK Toán 8 Tập 1
Bài tập 41 trang 88 SGK Toán 8 Tập 1
Bài tập 42 trang 89 SGK Toán 8 Tập 1
Bài tập 60 trang 86 SBT Toán 8 Tập 1
Bài tập 61 trang 87 SBT Toán 8 Tập 1
Bài tập 62 trang 87 SBT Toán 8 Tập 1
Bài tập 63 trang 87 SBT Toán 8 Tập 1
Bài tập 64 trang 87 SBT Toán 8 Tập 1
Bài tập 65 trang 87 SBT Toán 8 Tập 1
Bài tập 66 trang 87 SBT Toán 8 Tập 1
Bài tập 67 trang 87 SBT Toán 8 Tập 1
Bài tập 68 trang 87 SBT Toán 8 Tập 1
Bài tập 69 trang 88 SBT Toán 8 Tập 1
Bài tập 70 trang 88 SBT Toán 8 Tập 1
Bài tập 71 trang 88 SBT Toán 8 Tập 1
Bài tập 72 trang 88 SBT Toán 8 Tập 1
-


Cho hình vuông ABCD cạnh bằng a. M và N là hai điểm lưu động lần lượt trên cạnh AB và AD sao cho Góc MCN bằng 45 độ. Vẽ tia Cx vuông góc với CN, Cx cắt đường thẳng AB tại E. Tính chu vi của tam giác AMN theo a.
bởi Mai Đào
 16/01/2021
16/01/2021
A. 4a
B. 3a
C. a
D. 2a
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, trong đó AB = 8cm, AC = 10cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
bởi Lam Van
 16/01/2021
16/01/2021
A. 38cm
B. 54cm
C. 36cm
D. 18cm
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, trong đó AB = 11cm, AC = 15cm. Vẽ hình đối xứng với tam giác ABC qua trục là cạnh BC. Chu vi của tứ giác tạo thành là:
bởi Hoàng giang
 15/01/2021
15/01/2021
A. 52cm
B. 54cm
C. 26cm
D. 51cm
Theo dõi (0) 1 Trả lời





