Giải bài 65 tr 87 sách BT Toán lớp 8 Tập 1
Tứ giác \(ABCD\) có \(AB = BC,\) \(CD = DA\) (hình cái diều). Chứng minh rằng điểm \(A\) đối xứng với điểm \(C\) qua đường thẳng \(BD.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
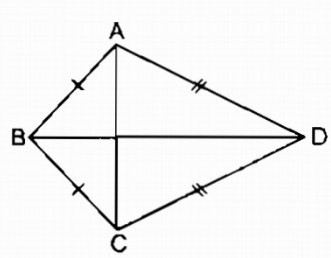
Ta có: \(BA = BC\;\;\;(gt)\)
Suy ra \(B\) thuộc đường trung trực của \(AC\)
\(DC = DA\;\;\; (gt)\)
Suy ra \(D\) thuộc đường trung trực của \(AC\)
Mà \(B ≠ D\) nên \(BD\) là đường trung trực của \(AC\)
Do đó \(A\) đối xứng với \(C\) qua đường thẳng \(BD.\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 63 trang 87 SBT Toán 8 Tập 1
Bài tập 64 trang 87 SBT Toán 8 Tập 1
Bài tập 66 trang 87 SBT Toán 8 Tập 1
Bài tập 67 trang 87 SBT Toán 8 Tập 1
Bài tập 68 trang 87 SBT Toán 8 Tập 1
Bài tập 69 trang 88 SBT Toán 8 Tập 1
Bài tập 70 trang 88 SBT Toán 8 Tập 1
Bài tập 71 trang 88 SBT Toán 8 Tập 1
Bài tập 72 trang 88 SBT Toán 8 Tập 1
-


Cho tam giác ABC gọi M là trung điểm của BC. Gọi H và K theo thứ tự là hình chiếu của B và C trên AM. Chứng minh rằng CH//BK
Theo dõi (0) 1 Trả lời -


Tìm các chữ in hoa có đối xứng trục
bởi thuy linh
 31/08/2019
31/08/2019
Các chữ in hoa có đối xứng trục
Theo dõi (0) 1 Trả lời -


Cho tứ giác ABCD có góc ngoài tại đỉnh C= góc ACB. Chứng minh AB+BD> AC+CD
Theo dõi (0) 1 Trả lời






