Giải bài 72 tr 88 sách BT Toán lớp 8 Tập 1
Cho góc nhọn xOy, điểm A nằm trong góc đó. Dựng điểm B thuộc tia Ox, điểm C thuộc tia Oy sao cho tam giác ABC có chu vi nhỏ nhất.
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng tính chất đường trung trực: Điểm cách đều hai đầu mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
Lời giải chi tiết
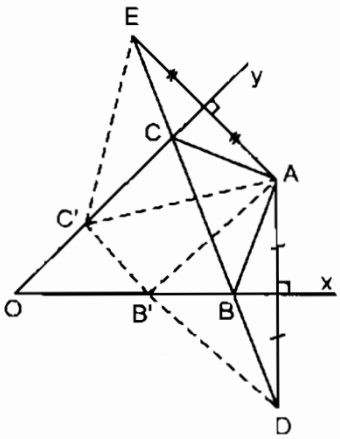
Cách dựng:
- Dựng điểm \(D\) đối xứng với \(A\) qua \(Ox\)
- Dựng điểm \(E\) đối xứng với \(A\) qua tia \(Oy\)
- Nối \(DE\) cắt \(Ox\) tại \(B, Oy\) tại \(C\)
Tam giác \(ABC\) là tam giác có chu vi nhỏ nhất.
Vì \(\widehat {xOy} < {90^0}\) nên \(DE\) luôn cắt \(Ox\) và \(Oy\) do đó \(∆ ABC\) luôn dựng được.
Chứng minh:
Chu vi \(∆ ABC\) bằng \(AB + BC + AC\)
Vì \(D\) đối xứng với \(A\) qua \(Ox\) nên \(Ox\) là đường trung trực của \(AD\)
\(⇒ AB = BD\) ( tính chất đường trung trực)
\(E\) đối xứng với \(A\) qua \(Oy\) nên \(Oy\) là đường trung trực của \(AE\)
\(⇒AC = CE\) ( tính chất đường trung trực)
Suy ra: \(AB + BC + AC \)\(= BD + BC + CE = DE \;\;(1)\)
Lấy \(B’\) bất kì trên \(Ox,\) \(C’\) bất kì trên tia \(Oy.\) Nối \(C’E,\) \(C’A,\) \(B’A,\) \(B’D.\)
Ta có: \(B’A = B’D\) ( tính chất đường trung trực)
\(C’A = C’E\) (tính chất đường trung trực)
Chu vi \(∆ AB’C’\) bằng \(AB’ + AC’ + B’C’\)\( = B’D + B’C’ +C’E \;\;(2)\)
Vì \(DE ≤ B’D + B’C’ + C’E\) (dấu bằng sảy ra khi \(B’\) trùng \(B,\) \(C’\) trùng \(C\))
nên chu vi của \(∆ ABC ≤\) chu vị của \(∆ A’B’C’\)
Vậy \(∆ ABC\) có chu vi bé nhất.
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Chứng minh E, F, G đối xứng với H qua BC, AC, AB biết tam giác ABC có các đường cao AM, BN
bởi Nguyễn Quỳnh Anh
 21/11/2017
21/11/2017
Giúp em bốn bài này với ạ
.jpg) Theo dõi (0) 3 Trả lời
Theo dõi (0) 3 Trả lời





