Giải bài 60 tr 86 sách BT Toán lớp 8 Tập 1
Cho tam giác \(ABC\) có \(\widehat A = {70^0}\), điểm \(M\) thuộc cạnh \(BC.\) Vẽ điểm \(D\) đối xứng với \(M\) qua \(AB,\) vẽ điểm \(E\) đối xứng với \(M\) qua \(AC.\)
\(a)\) Chứng minh rằng \(AD = AE.\)
\(b)\) Tính số đo góc \(DAE.\)
Hướng dẫn giải chi tiết
Hướng dẫn giải
+) Sử dụng định nghĩa: Hai điểm gọi là đối xứng với nhau qua đường thẳng \(d\) nếu \(d\) là đường trung trực của đoạn thẳng nối hai điểm đó.
+) Sử dụng tính chất đường trung trực: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai đầu mút của đoạn thẳng đó.
+) Trong tam giác cân, đường trung tuyến ứng với cạnh đáy cũng là đường trung trực, đường phân giác.
Lời giải chi tiết
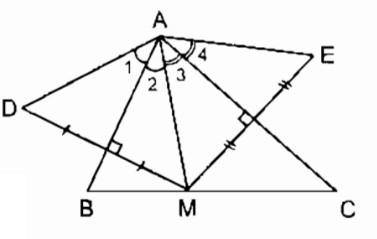
\(a)\) Vì \(D\) đối xứng với \(M\) qua trục \(AB\)
\(⇒ AB\) là đường trung trực của \(MD.\)
\(⇒ AD = AM\) (tính chất đường trung trực) \((1)\)
Vì \(E\) đối xứng với \(M\) qua trục \(AC\)
\(⇒ AC\) là đường trung trực của \(ME\)
\(⇒ AM = AE\) ( tính chất đường trung trực) \((2)\)
Từ \((1)\) và \((2)\) suy ra : \(AD = AE\)
\(b)\) \(AD = AM\) suy ra \(∆ AMD\) cân tại \(A\) có \(AB ⊥ MD\) nên \(AB\) cũng là đường phân giác của góc \(MAD\)
\( \Rightarrow {\widehat A_1} = {\widehat A_2}\)
\(AM = AE\) suy ra \(∆ AME\) cân tại \(A\) có \(AC ⊥ ME\) nên \(AC\) cũng là đường phân giác của \(\widehat {MAE}\)
\( \Rightarrow {\widehat A_3} = {\widehat A_4}\)
\(\widehat {DAE} = {\widehat A_1} + {\widehat A_2} + {\widehat A_3} + {\widehat A_4}\)
\(= 2\left( {{{\widehat A}_2} + {{\widehat A}_3}} \right) \)\(= 2\widehat {BAC}\)\( = {2.70^0} = {140^0}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
Bài tập 41 trang 88 SGK Toán 8 Tập 1
Bài tập 42 trang 89 SGK Toán 8 Tập 1
Bài tập 61 trang 87 SBT Toán 8 Tập 1
Bài tập 62 trang 87 SBT Toán 8 Tập 1
Bài tập 63 trang 87 SBT Toán 8 Tập 1
Bài tập 64 trang 87 SBT Toán 8 Tập 1
Bài tập 65 trang 87 SBT Toán 8 Tập 1
Bài tập 66 trang 87 SBT Toán 8 Tập 1
Bài tập 67 trang 87 SBT Toán 8 Tập 1
Bài tập 68 trang 87 SBT Toán 8 Tập 1
Bài tập 69 trang 88 SBT Toán 8 Tập 1
Bài tập 70 trang 88 SBT Toán 8 Tập 1
Bài tập 71 trang 88 SBT Toán 8 Tập 1
Bài tập 72 trang 88 SBT Toán 8 Tập 1
-


Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của hai đường chéo. I là trung điểm của đường trung bình của hình thang. Chứng minh rằng đường thẳng OI là trục đối xứng của hình thang.
Giup mình với nha!!!!!!! Mình đang cần gấp
Theo dõi (0) 1 Trả lời -


Nối mỗi cột của ô bên trái với một ô bên phải
bởi thanh hằng
 31/05/2019
31/05/2019
Hãy nối mỗi cột của ô bên trái với một ô của cột bên phải để được khẳng định đúng.
1. Trục đối xứng của tam giác ABC (AB = BC) là
A. đường trung trực của AB.
2. Trục đối xứng của hình thang cân ABCD (AB // CD) là
B. đường trung trực của BC.
C. đường trung trực của AC.
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC nhọn, M là 1 điểm thuộc BC, gọi D và E lần lượt là điểm đối xứng của M qua AB, AC.
a. Cm: \(\Delta ADE\) cân (đã làm)
b. DE cắt AB và AC theo thứ tự ở I và K. Cm MA là p/g của \(\widehat{IMK}\)
c. Biết \(\widehat{BAC}=70^o.\) Tính các góc của \(\Delta ADE\)
Ps: Mk đã làm ý a rồi nhé, các bạn giúp mk ý b và ý c nha :)
@Nguyễn Huy Tú, @soyeon_Tiểubàng giải, .... và các bn khác giúp mk nhé!
Theo dõi (0) 1 Trả lời






