Giải bài 17 tr 81 sách BT Toán lớp 8 Tập 1
Cho tam giác ABC. Các tia phân giác của các góc B và C cắt nhau ở I. Qua I kẻ đường thẳng song song với BC, cắt các cạnh AB và AC ở D và E.
a. Tìm các hình thang trong hình vẽ
b. Chứng minh rằng hình thang BDEC có một cạnh đáy bằng tổng hai cạnh bên.
Hướng dẫn giải chi tiết
Hướng dẫn giải
a. Sử dụng định nghĩa: Hình thang là tứ giác có hai cạnh đối song song.
b. Sử dụng tính chất hai góc so le trong, tam giác cân.
Lời giải chi tiết
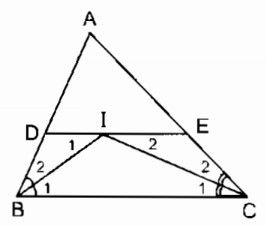
a. Đường thẳng đi qua I song song với BC cắt AB tại D và AC tại E, ta có các hình thang sau: BDEC, BDIC, BIEC.
b. DE // BC (theo cách vẽ)
\( \Rightarrow {\widehat I_1} = {\widehat B_1}\) (hai góc so le trong)
Mà \({\widehat B_1} = {\widehat B_2}\) (gt)
Suy ra: \({\widehat I_1} = {\widehat B_2}\)
Do đó: ∆ BDI cân tại D
⇒ DI = DB (1)
Ta có: \({\widehat I_2} = {\widehat C_1}\) (so le trong)
\({\widehat C_1} = {\widehat C_2}\) (gt)
Suy ra: \({\widehat I_2} = {\widehat C_2}\) do đó: ∆ CEI cân tại E
⇒ IE = EC (2)
DE = DI + IE (3)
Từ (1), (2) và (3) suy ra: DE = BD + CE
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-


Chứng minh AB = BC biết hình thang ABCD có AD//BC
bởi Bo Bo
 14/01/2018
14/01/2018
Cho hình thang ABCD ( AD song song BC ) . Gọi AC là tia phân giác của góc A . CM: AB = BC
giúp mk vs
Theo dõi (0) 1 Trả lời -


Chứng minh tam giác IDF cân biết tam giác ABC có AB>AC
bởi Nhat nheo
 27/07/2018
27/07/2018
cho tam giác ABC ,AB lớn hơn AC . trên cạnh AC lấy điểm E sao cho BE=AC.Gọi I,D,F theo thứ tự là trun g điểm của CE,AE,DC .Chứng minh
a) tam giác IDF cân
b) Góc BAC =2 lần góc IDF
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, đường cao AH, kẻ HE ⊥ AB tại E, kéo dài HE lấy EM = EH. Kẻ HF ⊥ AC tại F, kéo dài HF lấy FN = FH. Gọi I là trung điểm của MN. Chứng minh:
a) AB là trung trực của MH. AC là trung trực của NH
b) Tam giác AMN cân
c) EF song song MN
d) AI ⊥ EF
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuong cân tại A, tren AB lấy D ,tren AC lấy E sao cho AD=AE.Từ C kẻ đường vuông góc với BE cắt AB tại I
a)Cm:BE=IC
b)Qua D và A vẽ đường vuông góc với BE cắt BC tại M và N.CM:MN=CN
Theo dõi (0) 1 Trả lời -
ADMICRO


Tính các góc của hình thang ABCD có AB//CD
bởi Nguyễn Thị Thanh
 02/04/2019
02/04/2019
Mọi người giải bài này giuos mình với ạ
Cho hình thang ABCD (AB//CD) có:
Góc A-D= 20 độ
Góc B=2 lần góc C
Tính các góc của hình thang
ai giải đc giúp mình với ạ. cảm ơn
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC vuông cân A. Trên AB lấy D, trên cạnh AC lấy điểm E sao cho AD=AE. Từ C kẻ đường thẳng vuông góc BE cắt BA tại I. Chứng minh: a) BE=CI
Cho tam giác ABC vuông cân A. Trên AB lấy D, trên cạnh AC lấy điểm E sao cho AD=AE. Từ C kẻ đường thẳng vuông góc BE cắt BA tại I. Chứng minh: a) BE=CI b)Qua D và A kẻ đường thẳng vuông góc với BE cắt BC lần lượt tại M, N. Chứng minh MN=NC
b)Qua D và A kẻ đường thẳng vuông góc với BE cắt BC lần lượt tại M, N. Chứng minh MN=NC
Theo dõi (0) 1 Trả lời -


Chứng minh ABCD là hình thang biết tứ giác ABCD có BC=CD và BD là tia phân giác của góc D
bởi Choco Choco
 23/01/2018
23/01/2018
Bài 1: Tính các góc của hình thang ABCD(AB//CD), biết rằng A=4D, B-C=40O
Bài 2: Tứ giác ABCD có BC=CD và BD là tia phân giác của góc D. Chứng minh rằng:ABCD là hình thang.
Bài 3: Cho hình thang ABCD có A=100o, C=70o và cạnh đáy AB bằng cạnh bên AD. C/m tam giác DBC cân.
Theo dõi (0) 1 Trả lời -


Chứng minh MN//CD biết hình thang ABCD có phân giác góc ngoài tại đỉnh A và D cắt nhau ở M
bởi Duy Quang
 26/05/2018
26/05/2018
Cho hình thang ABCD(AB//CD).Các phân giác góc ngoài tại đỉnh A và D cắt nhau ở M,Các phân giãcy của góc ngoài tại đỉnh B và C cắt nhau ở N.
a)Chứng minh MN//CD
b)Biết MN=4.Tính chu vi h/thang ABCD
Theo dõi (0) 1 Trả lời -


cho tam giác abc vuông tại a,ab=12cm,bc=13cm.Gọi m,n là trung điểm của ab và bc.
a)CM:mn vuông góc ab
b)tính độ dài mn.
lưu ý nhớ vẽ hình
Theo dõi (0) 1 Trả lời -


Chứng minh hình thang có nhiều nhất 2 góc tù
bởi Nguyễn Thị Thu Huệ
 06/02/2018
06/02/2018
Chứng minh rằng trong hình thang có nhiều nhất hai góc tù, có nhiều nhất hai góc nhọn
Theo dõi (0) 1 Trả lời -


Chứng minh AM là tia phân giác góc A
bởi Mai Vàng
 26/05/2018
26/05/2018
Các bạn giúp mik vơi mik cần gấp lắm!
Cho hình thang ABCD (AB//CD), M là trung điểm của BC, cho biết DM là tia phân giác góc D. Chứng minh AM là tia phân giác góc A
Theo dõi (0) 1 Trả lời -


Hình thang ABCD có AB song song với CD, AB=a ,BC=b.CD=c,DA=d.Các đường phân giác của các góc ngoài tại đỉnh A và D cắt nhau tại M, các đường phân giác của các góc ngoài tại đỉnh B và C cắt nhau tại M .
a, cm MN song song với CD
b,tính độ dài cạnh MN theo a, b, c, d (cùng đơn vị)
giúp mk ạ mk cần lúc 12 h ạ
 Theo dõi (0) 1 Trả lời
Theo dõi (0) 1 Trả lời -


Chứng minh DMEH là hình thang cân
bởi Nguyễn Thị Thanh
 13/07/2018
13/07/2018
Cho hình thang ABCD ( AB//CD và ^A = 90*).Biết AB=AD=\(\dfrac{1}{2}\)CD.Kẻ BH\(\perp\)CD cắt AC tại E.Từ E kẻ đường thẳng // với AB cắt BD tại F,cắt AD tại M.Chứng minh:
a, MF=CH
b, tứ giác DMEH là hình thang cân
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC, các đường trug tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE và CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. CMR: MI = IK = KN
Theo dõi (0) 1 Trả lời -


Chứng minh DE//IK, DE=IK biết tam giác ABC có đường trung tuyến BD và CE cắt nhau ở G
bởi minh dương
 19/03/2018
19/03/2018
1 cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau ở G. Gọi I, K theo thứ tự là trung điểm của GB, GC. Chứng minh rằng DE//IK, DE=IK
2 Cho tam giác ABC, đường trung tuyến AM, E là giao điểm BD và AC. CMR: AE = \(\dfrac{1}{2}\) EC
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC. Các đường trung tuyến BD và CE. Lấy M,N thuộc BC sao cho BM=MN=NC. I là giao điểm của AM với BD. K là giao điểm của AN với CE. Cho BC=a. Tính IK theo a.
Các bạn giúp mình với!Thanks!
Theo dõi (0) 1 Trả lời -


Cho tam giác ABC và trọng tâm G. Vẽ đường thẳng d đi qua điểm G cắt cạnh AB, AC Gọi A', B', C' là hình chiếu lần lượt của A, B, C trên d Tìm mối liên hệ giữa AA', BB', CC'
Theo dõi (0) 1 Trả lời -


Tính DE biết tam giác vuông ABC có AB=8cm, BC=17cm
bởi Hương Lan
 25/04/2018
25/04/2018
Cho tam giác vuông ABC có AB=8cm;BC=17cm.Vẽ vào bên trong tam giác ABC 1 tam giác vuông cân DAB có cạnh huyền AB.Gọi E là trung điểm BC.Tính DE
Theo dõi (0) 1 Trả lời -


Cho một hình thang có hai đáy không bằng nhau.
Chứng minh rằng tổng hai góc kề đáy nhỏ lớn hơn tổng hai góc kề đáy lớn.Theo dõi (0) 1 Trả lời






