Với bài học này chúng ta sẽ tìm hiểu về Định lí Ta-lét (Thalès) trong tam giác. Đây là một định lí cực kì quan trọng trong chương trình toán phổ thông.
Tóm tắt lý thuyết
1.1. Định lí Talet trong tam giác
a. Định lí thuận
Nếu một đường thẳng cắt hai của một tam giác và song song với cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
\(\Delta ABC;\,\,B'C'\,//BC\, \Rightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}}.\)
b. Định lí đảo
Nếu một đường thẳng cắt hai cạnh của tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
\(\Delta ABC;\,\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow B'C'//BC\)
Tóm tắt: \(\Delta ABC;\,\,B'C'//BC \Leftrightarrow \frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}}.\)
Chú ý: Định lí Talet thuận và đảo đúng với cả ba trường hợp hình vẽ sau:
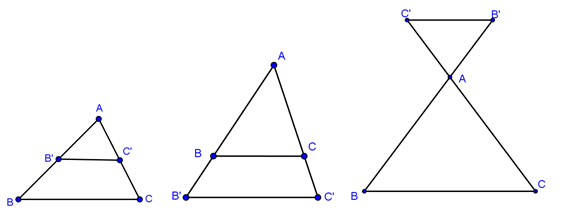
c. Hệ quả
Một đường thẳng cắt hai cạnh của tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
\(\Delta ABC;\,\,B'C'//BC \Rightarrow \frac{{AB'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{C'A}}{{CA}}.\)
1.2. Định lí Talet tổng quát
a. Định lí thuận
Nhiều đường thẳng song song định ra trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ.
\(a//\,\,b\,\,//\,\,c \Rightarrow \frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\)
Chú ý: Ta chứng minh dễ dàng định lí này bằng cách kẻ qua A’ một đường thẳng song song với \(\Delta \), đường này cắt b, c theo thứ tự tại các điểm B’’ và C’’. Dễ thấy A’B’’ = AB, B’’C’’ = BC. Sau đó, áp dụng định lí Talet trong tam giác vào tam giác A’C’’C’ để có:
\(\frac{{A'B'}}{{B'C'}} = \frac{{A'B''}}{{B''C''}}.\)
Từ đây suy ra kết luận.
.png)
b. Định lí đảo
Cho ba đường thẳng a, b, c cắt hai cát tuyến \(\Delta ,\,\,\Delta '\) tại các điểm theo thứ tự A, B, C và A’, B’, C’ thoả mãn đẳng thức tỉ lệ:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\)
Và hai trong ba đường thẳng a, b, c là song song với nhau thì đường thẳng còn lại cũng song song với hai đường kia.
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) và \(a//b \Rightarrow a//b//c\)
c. Hệ quả (Các đường thẳng đồng quy cắt hai đường thẳng song song)
- Nhiều đường thẳng đồng quy định ra trên hai đường thẳng song song những đoạn thẳng tương ứng tỉ lệ.
\(a//b \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{AC}}{{A'C'}}.\)
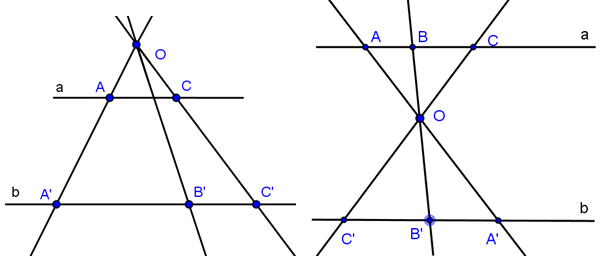
- Ngược lại, nếu nhiều đường thẳng định ra trên hai đường thẳng song song các đoạn thẳng tương ứng tỉ lệ thì chúng đồng quy tại một điểm.
\(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} \Rightarrow {\rm{AA}}',BB',CC'\) đồng quy tại O.
Việc chứng minh mệnh đề thuận được dựa trực tiếp vào định lí thuận của định lí Talet
Việc chứng minh mệnh đề đảo thường được nhờ vào phương pháp chứng minh phản chứng.
Chú ý:
1. Người ta thường sử dụng định lí Talet vào việc chứng minh các hệ thức dạng.
\(\begin{array}{l}\frac{a}{b} = \frac{c}{d}\\a.d = b.c\\{a^2} = b.c\end{array}\)
Nhất là khi trong giả thiết cho ta các đường thẳng song song.
2. Định lí đảo của định lí Talet cho ta một cách chứng minh hai đường thẳng song song.
3. Hệ quả của định lí Talet tổng quá cho ta cách chứng minh các đường thẳng đồng quy.
Ví dụ 1: Cho tam giác ABC. Trên cạnh AC ta lấy hai điểm D, E sao cho AD = DE = EC. Trung tuyến AM cắt BD tại P và trung tuyến CN cắt BE tại Q.
1. Chứng minh điểm Q là trung điểm của trung tuyến CN.
2. Chứng minh PQ // AC.
3. Suy ra \(PQ = \frac{1}{2}MN\) và \(PQ = \frac{3}{4}DE.\)
Giải
.png)
1. Nối AD. Vì N là trung điểm của AB, D là trung điểm của AE nên ND // BE hay QE // ND.
QE // ND mà E là trung điểm của CD nên suy ra Q là trung điểm của CN.
2. Lí luận như trên, ta chứng minh được P là trung điểm của AM.
Gọi G là trọng tâm của tam giác ABC. Như vậy
\(AG = \frac{2}{3}AM,\,\,AP = \frac{1}{2}AM\)
Cho ta \(GP = AG - AP = \frac{2}{3}AM - \frac{1}{2}AM = \frac{1}{6}AM\)
\( \Rightarrow \frac{{GP}}{{GA}} = \frac{1}{6}AM:\frac{2}{3}AM = \frac{1}{4}\)
Chứng minh tương tự, ta có:
\(\frac{{GQ}}{{GC}} = \frac{1}{4}\) hay \(\frac{{GP}}{{GA}} = \frac{{GQ}}{{GC}} \Rightarrow PQ//AC.\)
3. PQ // AC mà MN // AC suy ra PQ // MN,
Cho ta \(\frac{{PQ}}{{MN}} = \frac{{GP}}{{GM}} = \frac{1}{6}AM:\frac{1}{3}AM \Rightarrow \frac{{PQ}}{{MN}} = \frac{1}{2}\)
\( \Rightarrow PQ = \frac{1}{2}MN\)
\(PQ = \frac{1}{2}MN\) mà \(MN = \frac{1}{2}AC \Rightarrow PQ = \frac{1}{4}AC\)
Vì \(PQ = \frac{1}{4}AC\) và \(DE = \frac{1}{3}AC \Rightarrow \frac{{PQ}}{{DE}} = \frac{3}{4}\)
\( \Rightarrow PQ = \frac{3}{4}DE.\)
Ví dụ 2: Cho tứ giác lồi ABCD. Đường thẳng qua B và song song với CD cắt AC tại F bà đường thẳng qua C song song với AB cắt BD tại E. Chứng minh EF // AD.
Giải
.png)
Gọi O là giao điểm của hai đường chéo AC và BD
Áp dụng định lí Talet thuận vào tam giác AOB.
\(\begin{array}{l}EC//AB \Rightarrow \frac{{OC}}{{OA}} = \frac{{OE}}{{OB}}\\ \Rightarrow OC.OB = OA.OE\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1)\end{array}\)
Áp dụng định lí Talet thuận vào tam giác COD:
\(\begin{array}{l}FB//DC \Rightarrow \frac{{OC}}{{{\rm{OF}}}} = \frac{{OD}}{{OB}}\\ \Rightarrow OC.OB = OD.{\rm{OF}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm{(2)}}\end{array}\)
Từ (1) và (2) suy ra: \(OA.OE = OD.{\rm{OF}} \Rightarrow \frac{{OA}}{{OF}} = \frac{{OD}}{{OE}}\) (3)
Từ đẳng thức (3) theo định lí Talet đảo, ta có ngay EF // AD.
Ví dụ 3: Cho góc nhọn xOy. Trên cạnh Ox lấy hai điểm D, E. Một đường thẳng \({d_1}\) qua D cắt cạnh Oy tại điểm F, đường thẳng \({d_2}\) đi qua E và song song với \({d_1}\), cắt cạnh Oy tại điểm G. Đường thẳng \({d_3}\)qua G và song song với EF, cắt cạnh Ox tại điểm H. Chứng minh hệ thức: \(O{E^2} = OD.OH.\)
Giải
.png)
Áp dụng định lí Talet thuận vào tam giác OEG:
\(FD\,\,//\,\,EG \Rightarrow \frac{{OD}}{{OE}} = \frac{{{\rm{OF}}}}{{OG}}\,\,\,\,(1)\)
Với tam giác OGH, ta có:
\(GH//FE \Rightarrow \frac{{OF}}{{OG}} = \frac{{OE}}{{OH}}\,\,\,\,(2)\)
Từ (1) và (2) suy ra: \(\frac{{OE}}{{OH}} = \frac{{OD}}{{OE}} \Rightarrow O{E^2} = OD.OH\)
Bài tập minh họa
Bài 1: Cho hình thang ABCD, đáy lớn AB. Từ đỉnh C, kẻ đường thẳng song song với AD, đường này cắt BD tại P và cắt AB tại E. Qua D, kẻ đường thẳng song song với BC, đường này cắt AC tại N và cắt AB tại F. Đường thẳng qua E song song với AC cắt BC tại Q và đường thẳng qua F song song với BD cắt AD tại M.
1. Chứng minh bốn điểm M, N, P, Q nằm trên một đường thẳng song song với hai đáy.
2. Chứng minh MN = PQ
3. Cho AB = a, DC = b. Chứng minh rằng các điểm M, N, P, Q theo thứ tự chia các đoạn thẳng AD, AC, BD, BC theo cùng một tỉ số k. Tính k theo a, b.
Giải
.png)
1. Ta có:
\(MF//DB \Rightarrow \frac{{AM}}{{DM}} = \frac{{{\rm{AF}}}}{{FB}}\)
Mà FB = DC nên \(\frac{{AM}}{{DM}} = \frac{{{\rm{AF}}}}{{DC}}\,\,\,\,(1)\)
\(DC{\rm{ }}//{\rm{ }}AF \Rightarrow \frac{{AF}}{{DC}} = \frac{{AN}}{{NC}}\,\,\,\,(2)\)
Từ (1) và (2) suy ra \(\frac{{AM}}{{DM}} = \frac{{AN}}{{NC}}\)
\( \Rightarrow MN\,\,\,//DC\,\,\,\,\,\,\,\,\,\,\,(3)\)
Tương tự, ta có: PQ // DC (4)
\(MN//\,\,DC \Rightarrow MN//\,\,AF \Rightarrow \frac{{AM}}{{MD}} = \frac{{FN}}{{ND}}.\)
Dễ thấy \(\frac{{FN}}{{ND}} = \frac{{BQ}}{{QC}}\)
Vậy \(\frac{{AM}}{{MD}} = \frac{{BQ}}{{QC}} \Rightarrow MQ//DC\)
Từ (3), (4), (5) theo tiêu đề Ơclit, ta suy ra bốn điểm M, N, P, Q nằm trên cùng một đường thẳng song song với DC.
2. Ta có: \(\frac{{MN}}{{DC}} = \frac{{AM}}{{AD}};\,\,\frac{{PQ}}{{DC}} = \frac{{BQ}}{{BC}}\,\, \Rightarrow \frac{{MN}}{{DC}} = \frac{{PQ}}{{DC}} \Rightarrow MN = PQ.\)
3. Dễ thấy \(\frac{{MA}}{{MD}} = \frac{{NA}}{{NC}} = \frac{{PB}}{{PD}} = \frac{{QB}}{{QC}} = \frac{{{\rm{AF}}}}{{DC}} = \frac{{a - b}}{b}.\)
Bài 2: Cho hình thang ABCD đáy lớn CD; O là giao điểm của hai đường chéo. Đường thẳng qua A song song với BC cắt BD ở E và đường thẳng qua B song song với AD cắt đường thẳng AC tại F.
1. Chứng minh EF // AB.
2. Chứng minh hệ thức \(A{B^2}{\rm{ = EF}}{\rm{.CD}}\)
3. Gọi \({S_1},{S_2},{S_3},{S_4}\) theo thứ tự là diện tích các tam giác OAB, OCD, OAD và OBC. Chứng minh hệ thức: \({S_1}.{S_2} = {S_3}.{S_4}.\)
Giải
.png)
1. Ta có
\(\begin{array}{l}AE//BC \Rightarrow \frac{{OE}}{{OB}} = \frac{{OA}}{{OC}}\,\,\,(1)\\BF//AD \Rightarrow \frac{{OF}}{{OA}} = \frac{{OB}}{{OD}}\,\,\,(2)\\AB//DC \Rightarrow \frac{{OA}}{{OC}} = \frac{{OB}}{{OD}}\,\,\,(3)\end{array}\)
Từ (1), (2) và (3) suy ra \(\frac{{OE}}{{OB}} = \frac{{OF}}{{OA}} \Rightarrow {\rm{EF}}//BC.\)
2. Dễ thấy AB = MC = DN
\(AM//BC \Rightarrow \frac{{CD}}{{MC}} = \frac{{DB}}{{EB}}\)
Vì MC = AB nên từ đây, ta có \(\frac{{CD}}{{AB}} = \frac{{DB}}{{EB}}\) (4)
\({\rm{EF//DC}} \Rightarrow \frac{{DN}}{{EF}} = \frac{{DB}}{{EB}}\)
Vì DN = AB nên từ đây, ta có \(\frac{{AB}}{{EF}} = \frac{{DB}}{{EB}}\,\,\,\,(5)\)
Từ (4) và (5) suy ra \(\frac{{AB}}{{EF}} = \frac{{CD}}{{AB}} \Rightarrow A{B^2}{\rm{ = EF}}{\rm{.CD}}\)
3. Ta có
\(\begin{array}{l}\frac{{{S_{OAB}}}}{{{S_{OBC}}}} = \frac{{OA}}{{OC}};\frac{{{S_{OAD}}}}{{{S_{OCD}}}} = \frac{{OA}}{{OC}} \Rightarrow \frac{{{S_{OAB}}}}{{{S_{OBC}}}} = \frac{{{S_{OAD}}}}{{{S_{OCD}}}}\\ \Rightarrow {S_1}.{S_2} = {S_3}.{S_4}\end{array}\)
Bài 3: Cho tam giác ABC. Kẻ trung tuyến AM. Lấy một điểm D bất kì trên đoạn thẳng AM, J là giao điểm của BD và AC; I là giao điểm của CD và AB. Chứng minh IJ // BC.
Giải
.png)
Từ M kẻ đường thẳng song song với DC cắt AB ở P và kẻ đường thẳng song song với DB cắt AC ở Q. Dễ thấy.
IP = PB; JQ = QC
Ta có \(MP//CI \Rightarrow \frac{{AI}}{{AP}} = \frac{{AD}}{{AM}}\)
\(MQ//BJ \Rightarrow \frac{{{\rm{AJ}}}}{{AQ}} = \frac{{AD}}{{AM}}\)
Suy ra \(\frac{{AI}}{{AP}} = \frac{{{\rm{AJ}}}}{{AQ}} \Rightarrow {\rm{IJ}}//PQ\,\,\,(1)\)
Ta lại có MP // CI \( \Rightarrow \frac{{MA}}{{MD}} = \frac{{PA}}{{PI}}\) mà PI = PB
Nên \(\frac{{MA}}{{MD}} = \frac{{PA}}{{PB}}\)
Tương tự, ta có \(\frac{{MA}}{{MD}} = \frac{{QA}}{{QB}}\)
Vậy \(\frac{{PA}}{{PB}} = \frac{{QA}}{{QB}} \Rightarrow PQ//BC\)
Từ (1) và (2) suy ra IJ // BC.
3. Luyện tập Bài 1 Chương 3 Hình học 8
Qua bài giảng Định lí Ta-lét trong tam giác này, các em cần hoàn thành 1 số mục tiêu mà bài đưa ra như :
- Nắm vững định lí Ta - let trong tam giác và mở rộng hơn là định lí Ta - let tổng quát
- Vận dụng kiến thức giải được một số bài toán liên quan
3.1 Trắc nghiệm về Định lí Ta-lét trong tam giác
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Hình học 8 Chương 3 Bài 1 cực hay có đáp án và lời giải chi tiết.
-
- A. \(\frac{{AB}}{{C{\rm{D}}}} = \frac{1}{4}\)
- B. \(\frac{{AB}}{{C{\rm{D}}}} = \frac{1}{5}\)
- C. \(\frac{{AB}}{{C{\rm{D}}}} = \frac{1}{6}\)
- D. \(\frac{{AB}}{{C{\rm{D}}}} = \frac{1}{7}\)
-
- A. AB2 = AD.AF
- B. AB2 > AD.AF
- C. AB2 < AD.AF
- D. AB2 = 2. AD.AF
-
Câu 3:
Tìm độ dài x trong hình sau:
- A. 12 cm
- B. 20 cm
- C. 22 cm
- D. 24 cm
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!
3.2. Bài tập SGK về Định lí Ta-lét trong tam giác
Các em có thể xem thêm phần hướng dẫn Giải bài tập Hình học 8 Chương 3 Bài 1 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Bài tập 1 trang 58 SGK Toán 8 Tập 2
Bài tập 2 trang 59 SGK Toán 8 Tập 2
Bài tập 3 trang 59 SGK Toán 8 Tập 2
Bài tập 4 trang 59 SGK Toán 8 Tập 2
Bài tập 5 trang 59 SGK Toán 8 Tập 2
Bài tập 1 trang 82 SBT Toán 8 Tập 2
Bài tập 2 trang 82 SBT Toán 8 Tập 2
Bài tập 3 trang 82 SBT Toán 8 Tập 2
Bài tập 4 trang 83 SBT Toán 8 Tập 2
Bài tập 5 trang 83 SBT Toán 8 Tập 2
Bài tập 1.1 trang 83 SBT Toán 8 Tập 2
Bài tập 1.2 trang 83 SBT Toán 8 Tập 2
4. Hỏi đáp Bài 1 Chương 3 Hình học 8
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 8 HỌC247





.PNG)







