Giải bài 4 tr 83 sách BT Toán lớp 8 Tập 2
Cho hình thang ABCD có AB // CD và AB < CD
Đường thẳng song song với đáy AB cắt các cạnh bên CD, BC theo thứ tự tại M và N.
Chứng minh rằng:
a. \({{MA} \over {AD}} = {{NB} \over {BC}}\)
b. \({{MA} \over {MD}} = {{NB} \over {NC}}\)
c. \({{MD} \over {DA}} = {{NC} \over {CB}}\)
HD: Kéo dài các tia DA, CB cắt nhau tại E(h.3), áp dụng định lí Ta-lét trong tam giác và tính chất của tỉ lệ thức để chứng minh.
Hướng dẫn giải chi tiết
Hướng dẫn giải
a) Định lí Ta - lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
b) Áp dụng tính chất :
\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{b - a}} = \dfrac{c}{{d - c}}\)
c) Áp dụng tính chất :
\(\dfrac{a}{b} = \dfrac{c}{d} \Rightarrow \dfrac{a}{{b + a}} = \dfrac{c}{{d + c}}\)
Lời giải chi tiết
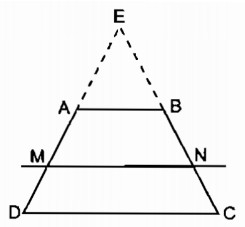
a) Gọi \(E\) là giao điểm của \(AD\) và \(BC.\)
Xét \(∆ EMN\) có \(AB // MN\) (gt)
Theo định lí Ta-lét ta có:
\(\displaystyle{{EA} \over {MA}} = {{EB} \over {NB}}\)
\(\Rightarrow \displaystyle{{EA} \over {EB}} = {{MA} \over {NB}}\) (1)
Xét \(∆ EDC\) có \(AB // CD\) (gt)
Theo định lí Ta-lét ta có:
\(\displaystyle{{EA} \over {AD}} = {{EB} \over {BC}}\)
\(\Rightarrow \displaystyle{{EA} \over {EB}} = {{AD} \over {BC}}\) (2)
Từ (1) và (2) suy ra: \(\displaystyle {{MA} \over {NB}} = {{AD} \over {BC}}\)
\(\displaystyle \Rightarrow {{MA} \over {AD}} = {{NB} \over {BC}}\)
b) Ta có \(\displaystyle{{MA} \over {AD}} = {{NB} \over {BC}}\) (câu a)
Suy ra:
\(\displaystyle{{MA} \over {AD - MA}} = {{NB} \over {BC - NB}}\)
\(\displaystyle \Rightarrow {{MA} \over {MD}} = {{NB} \over {NC}}\)
c) Ta có \(\displaystyle{{MA} \over {MD}} = {{NB} \over {NC}}\) (câu b)
\( \Rightarrow \dfrac{{MD}}{{MA}} = \dfrac{{NC}}{{NB}}\)
Suy ra:
\(\displaystyle {{MD} \over {MA + MD}} = {{NC} \over {NB + NC}} \)
\(\displaystyle \Rightarrow {{MD} \over {DA}} = {{NC} \over {CB}}\)
-- Mod Toán 8 HỌC247
Bài tập SGK khác
-
Tính AE/AD biết tam giác AEC có AB/BC=1/3, BD//CE
bởi Hoa Lan
31/05/2019
Cho tam giác AEC có AB/BC=1/3;BD//CE. Tính AE/Ad
Theo dõi (0) 1 Trả lời -
Tính chu vi tam giác ADE biết tam giác ABC cân tại A có AB=8cm, BC=4cm
bởi Phan Thiện Hải
31/05/2019
1. cho hình thang ABCD (AB//CD). một đường thẳng a song song vs AB, cắt AD, BC tại E và F. Chứng minh:
a) \(\dfrac{AE}{ED}\)=\(\dfrac{BF}{FC}\) b)\(\dfrac{DE}{DA}\)=\(\dfrac{FC}{BC}\)
2. cho tam giác ABC, D ∈ BC sao cho \(\dfrac{BD}{BC}\)=\(\dfrac{1}{4}\). E ∈ AD sao cho AE=2.ED. BE cắt AC tại K. Tính: \(\dfrac{AK}{KC}\)
3. cho tam giác ABC cân tại A có AB=8cm, BC=4cm. kẻ DE//BC (D ∈ AB, E ∈ AC). biết chu vi hình thag BDEC=7cm. Tính chu vi tam giác ADE.
mấy man làm giúp vs!!thanks nhiều:)
Theo dõi (0) 1 Trả lời -
cho tam giác abc có ab=12cm, ac=18cm và bc=27cm. Điểm d thuộc bc sao cho cd=12cm.Tính độ dài ad
giải dùm mình nhaTheo dõi (0) 1 Trả lời -
Tính độ dài x của đoạn thẳng có trong hình
bởi cuc trang
31/05/2019
1. Tính độ dài x của các đoạn thẳng trong hình 9
a) DE/BC b) MN//PQ c)
Theo dõi (0) 1 Trả lời -
ADMICRO
Chứng minh AE/AB + AF/AC = 1
bởi Việt Long
31/05/2019
cho tam giac ABC, D thuoc BC. Qua D ke cac duong thang song song voi AC va AB chung cat AB va AC lan luot o E va F. Chung minh rang: AE/AB + AF/AC = 1
Theo dõi (0) 1 Trả lời -
Tính BD,BE,ED biết AB=6cm,AC=9cm,BC=7.5 cm
bởi Anh Nguyễn
31/05/2019
Cho tam giác ABC, AB=6cm,AC=9cm,BC=7.5 cm, đường phân giác trong và ngoài của góc A cắt BC ở D và E.Tính BD,BE,ED.
Theo dõi (0) 1 Trả lời -
Chứng minh (AF:AB)+(AE:AC)=1
bởi hà trang
31/05/2019
Cho tam giác ABC, từ điểm D trên BCker các đường thẳng// với các cạnh AB,AC chúng cắt AB,AC theo thứ tự tai E,F
CMR: (AF:AB)+(AE:AC)=1
Theo dõi (0) 1 Trả lời
