Giải bài 1.2 tr 83 sách BT Toán lớp 8 Tập 2
Tam giác ABC vuông tại A có đường cao là AD (D ∈ BC). Từ D, kẻ DE vuông góc với AB (E ∈ AB) và DF vuông góc với AC (F ∈ AC).
Hỏi rằng, khi độ dài các cạnh AB, AC thay đổi thì tổng \({{AE} \over {AB}} + {{AF} \over {AC}}\) có thay đổi hay không ? Vì sao?.
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng:
- Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau.
- Định lí Ta-lét: Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ.
Lời giải chi tiết
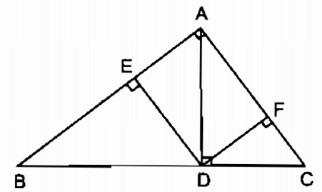
Vì \(DE\) và \(CA\) cùng vuông góc với \(AB\) nên \(DE // AC\).
Xét \(\Delta ABC\) có \(DE//AC\)
Theo định lí Ta-lét, ta có:
\(\displaystyle {{AE} \over {AB}} = {{CD} \over {CB}}\) (1)
Vì \(DF\) và \(BA\) cùng vuông góc với \(AC\) nên \(DF//AB\).
Xét \(\Delta ABC\) có \(DF//AB\)
Theo định lí Ta-lét, ta có:
\(\displaystyle {{AF} \over {AC}} = {{BD} \over {BC}}\) (2)
Cộng (1) và (2) theo vế với vế, ta có:
\(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}} = {{CD} \over {CB}} + {{BD} \over {BC}}\)
\(\displaystyle \Rightarrow {{AE} \over {AB}} + {{AF} \over {AC}}= {{CD + BD} \over {BC}}\)
\(\displaystyle \Rightarrow {{AE} \over {AB}} + {{AF} \over {AC}} = {{BC} \over {BC}} = 1\)
Tổng \(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}}\) không thay đổi vì luôn có giá trị bằng \(1.\)
Vậy khi độ dài cạnh góc vuông \(AB, AC\) của tam giác vuông \(ABC\) thay đổi thì tổng \(\displaystyle {{AE} \over {AB}} + {{AF} \over {AC}}\) luôn luôn không thay đổi. Tổng đó luôn có giá trị bằng \(1.\)
-- Mod Toán 8 HỌC247
-


Bài 5 trang 83 sách bài tập toán 8 tập 2
bởi hồng trang
 29/09/2018
Bài 5 (Sách bài tập - tập 2 - trang 83)
29/09/2018
Bài 5 (Sách bài tập - tập 2 - trang 83)Cho tam giác ABC. Từ điểm D trên cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AC và AB theo thứ tự tại F và E (h.4)
Chứng minh rằng :
\(\dfrac{AE}{AB}+\dfrac{AF}{AC}=1\)
Theo dõi (0) 1 Trả lời -


Bài 4 (Sách bài tập - tập 2 - trang 83)
bởi Thanh Nguyên
 23/12/2019
Bài 4 (Sách bài tập - tập 2 - trang 83)
23/12/2019
Bài 4 (Sách bài tập - tập 2 - trang 83)Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Theo dõi (0) 1 Trả lời -


Bài 3 trang 82 sách bài tập toán 8 tập 2
bởi hai trieu
 29/09/2018
Bài 3 (Sách bài tập - tập 2 - trang 82)
29/09/2018
Bài 3 (Sách bài tập - tập 2 - trang 82)Tính độ dài x của các đoạn thẳng trong hình 1, hình 2 biết rằng các số trên hình cùng đơn vị đo là cm ?
Theo dõi (0) 1 Trả lời -


Bài 2 (Sách bài tập - tập 2 - trang 82)
bởi Nguyễn Xuân Ngạn
 23/12/2019
Bài 2 (Sách bài tập - tập 2 - trang 82)
23/12/2019
Bài 2 (Sách bài tập - tập 2 - trang 82)Đoạn thẳng AB gập 5 làn đoạn thẳng CD; đoạn thẳng A'B' gấp 7 lần đoạn thẳng CD
a) Tính tỉ số của hai đoạn thẳng AB và A"B'
b) Cho biết đoạn thẳng MN = 505 cm và đoạn thẳng M'N' = 707 cm, hỏi hai đoạn thẳng AB, A'B' có tỉ lệ với hai đoạn thẳng MN và M'N' hay không ?
Theo dõi (0) 1 Trả lời -
ADMICRO

 Bài 1 (Sách bài tập - tập 2 - trang 82)
Bài 1 (Sách bài tập - tập 2 - trang 82)Viết tỉ số của các cặp đoạn thẳng sau :
a) AB = 125 cm, CD = 625 cm
b) EF = 45 cm, E'F' = 13,5 dm
c) MN = 555 cm, M'N' = 999 cm
d) PQ = 10101 cm, P'Q' = 303,03 m
Theo dõi (0) 1 Trả lời -


Tính CE biết BC // DE, AB = 2cm, AC = 3cm, BD = 4cm
bởi Lê Viết Khánh
 30/08/2019
30/08/2019
Cho hình, biết BC // DE, AB = 2cm, AC = 3cm, BD = 4cm. Tính CE?
Theo dõi (0) 1 Trả lời -


Cho hình, biết BC // DE, AB = 2cm, AC = 3cm, BD = 4cm. Tính CE?
Theo dõi (0) 1 Trả lời


