Luyện tập 2 trang 81 SGK Toán 7 Kết nối tri thức tập 2
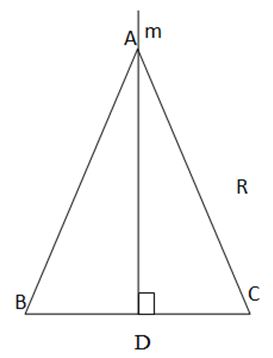
a) Chứng minh trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó
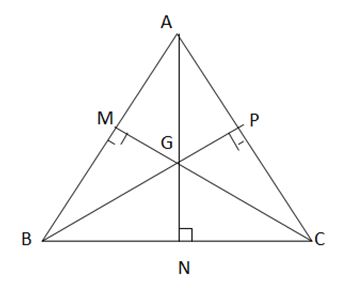
b) Chứng minh rằng trong tam giác đều, điểm cách đều ba đỉnh cũng cách đều ba cạnh của tam giác.
Hướng dẫn giải chi tiết Luyện tập 2
Phương pháp giải
Ba đường cao của một tam giác đồng quy tại một điểm.
Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó.
Lời giải chi tiết
a)
Gọi AD là đường trung tuyến và đường phân giác tại đỉnh A của ∆ ABC
xét ∆ ADB và ∆ ADC, có:
AB=AC
DB=DC
AD chung
=>∆ ADB = ∆ ADC
=> $\widehat{ADB}$ = $\widehat{ADC}$
Mà $\widehat{ADB}$ + $\widehat{ADC}$ = 180°
=> $\widehat{ADB}$ = $\widehat{ADC}$= 90°
=>AD vuông góc với BC
mà DA=DB
=>AD là đường trung trực của tam giác ABC
b)
G là điểm cách đều 3 đỉnh của tam giác ABC đều
GM, GN, GP là khoảng cách từ G đến AB, BC, AC
Xét ∆ AGB và ∆ AGC, có:
AG chung
GB= GC
AB= AC
=> ∆ AGB = ∆ AGC
=> $\widehat{GAB}$ = $\widehat{GAC}$
=> AG là đường phân giác của $\widehat{BAC}$
Tương tự ta có: CG là đường phân giác của $\widehat{ACB}$
=> G là điểm giao nhau giữa 2 đường phân giác AG và CG
=> G cách đều 3 cạnh AB,AC, BC.
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Luyện tập 1 trang 79 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Hoạt động 3 trang 79 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.26 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.27 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.28 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.29 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.30 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.19 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.20 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.21 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.22 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.