Giải bài 9.28 trang 81 SGK Toán 7 Kết nối tri thức tập 2
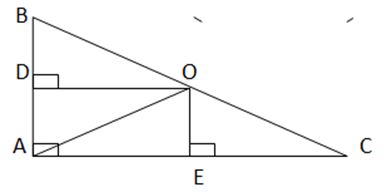
Xét điểm O cách đều 3 đỉnh của tam giác ABC. Chứng minh rằng nếu O nằm trên một cạnh của tam giác ABC thì ABC là một tam giác vuông
Hướng dẫn giải chi tiết Giải bài 9.28
Phương pháp giải
Xét ∆ OAB ta có : \(\widehat{OAB}\) + \(\widehat{OBA}\) + \(\widehat{AOB}\)= 180°
=> số đo \(\widehat{BAC}\)
Vậy ∆ ABC vuông tại A
Lời giải chi tiết
O cách đều 3 đỉnh của tam giác ABC => O là giao điểm của 3 đường trung trực của tam giác ABC
=> OA= OB= Oc
=> ∆ OAB cân tại O. => \(\widehat{OAB}\) = \(\widehat{OBA}\)
∆ OAC cân tại O => \(\widehat{OAC}\) + \(\widehat{OCA}\)
Xét ∆ OAB ta có : \(\widehat{OAB}\) + \(\widehat{OBA}\) + \(\widehat{AOB}\)= 180°
=> 2\(\widehat{OAB}\) + \(\widehat{AOB}\)= 180°
=> \(\widehat{AOB}\)= 180° - 2 \(\widehat{OAB}\)
Tương tự ta có \(\widehat{AOC}\)= 180° - 2 \(\widehat{OAC}\)
O thuộc BC => \(\widehat{AOB}\) + \(\widehat{AOC}\)= 180°
=.> 180° - 2 \(\widehat{OAB}\) + 180° - 2 \(\widehat{OAC}\) = 180°
=> 360° - 180° = 2 \(\widehat{OAB}\) + 2 \(\widehat{OAC}\)
=> 180° = 2 (\(\widehat{OAB}\) + \(\widehat{OAC}\) )
=> \(\widehat{BAC}\) = 90°
=> ∆ ABC vuông tại A
-- Mod Toán 7 HỌC247
Bài tập SGK khác
Giải bài 9.26 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.27 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.29 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.30 trang 81 SGK Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.19 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.20 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.21 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Giải bài 9.22 trang 58 SBT Toán 7 Kết nối tri thức tập 2 - KNTT
Chưa có câu hỏi nào. Em hãy trở thành người đầu tiên đặt câu hỏi.