B├ái tß║¡p trß║»c nghiß╗çm To├ín 12 B├ái 1 vß╗ü Sß╗æ phß╗®c online ─æß║ºy ─æß╗º ─æ├íp ├ín v├á lß╗Øi giß║úi gi├║p c├íc em tß╗▒ luyß╗çn tß║¡p v├á cß╗ºng cß╗æ kiß║┐n thß╗®c b├ái hß╗ìc.
Câu hỏi trắc nghiệm (10 câu):
-
Câu 1:
Cho sß╗æ phß╗®c \(z = ax + bi\,\left( {a,b \in R} \right)\), mß╗çnh ─æß╗ü n├áo sau ─æ├óy l├á sai?
- A. ─Éß╗æi vß╗øi sß╗æ phß╗®c z, a l├á phß║ºn thß╗▒c.
- B. ─Éiß╗âm \(M\left( {a,b} \right)\) trong mß╗Öt hß╗ç tß╗ìa ─æß╗Ö vu├┤ng g├│c cß╗ºa mß║Àt phß║│ng phß╗®c ─æã░ß╗úc gß╗ìi l├á ─æiß╗âm biß╗âu diß╗àn sß╗æ phß╗®c \(z = a + bi\).
- C. ─Éß╗æi vß╗øi sß╗æ phß╗®c z, bi l├á phß║ºn ß║úo.
- D. Sß╗æ i ─æã░ß╗úc gß╗ìi l├á ─æãín vß╗ï ß║úo.
-
- A. \(M\left( {5; - 3} \right)\)
- B. \(N\left( { - 3;5} \right)\)
- C. \(P\left( { - 5;3} \right)\)
- D. \(Q\left( {3; - 5} \right)\)
-
- A. Sß╗æ phß╗®c \(z=a+bi\) ─æã░ß╗úc biß╗âu diß╗àn bß║▒ng ─æiß╗âm M(a;b) trong mß║Àt phß║│ng phß╗®c Oxy
- B. Sß╗æ phß╗®c \(z=a+bi\)ÔÇï c├│ m├┤─æun l├á \(\sqrt {{a^2} + {b^2}}\)
- C. Sß╗æ phß╗®c \(z=a+bi\) th├¼ a=0 v├á b=0
- D. Sß╗æ phß╗®c \(z=a+bi\) c├│ sß╗æ phß╗®c li├¬n hß╗úp l├á \(\overline z = - a - bi\)
-
- A. ─Éã░ß╗Øng tr├▓n \({x^2} + {y^2} = 4\)
- B. ─Éã░ß╗Øng thß║│ng y=2
- C. ─Éã░ß╗Øng thß║│ng x=2
- D. Hai ─æã░ß╗Øng thß║│ng x=2 v├á y=2
-
Câu 5:
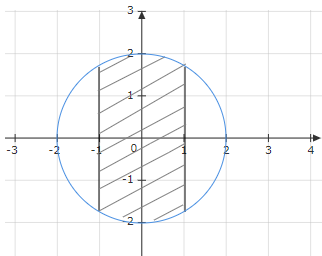
Sß╗æ phß╗®c thß╗Åa m├ún ─æiß╗üu kiß╗çn n├áo th├¼ c├│ ─æiß╗âm biß╗âu diß╗àn ß╗ƒ phß║ºn gß║ích ch├®o?
- A. Sß╗æ phß╗®c c├│ phß║ºn thß╗▒c nß║▒m trong \(\left( { - 1;1} \right)\) v├á m├┤ ─æun nhß╗Å hãín 2
- B. Sß╗æ phß╗®c c├│ phß║ºn thß╗▒c nß║▒m trong \(\left[ { - 1;1} \right]\) v├á m├┤ ─æun nhß╗Å hãín 2
- C. Sß╗æ phß╗®c c├│ phß║ºn thß╗▒c nß║▒m trong \(\left[ { - 1;1} \right]\) v├á m├┤ ─æun kh├┤ng vã░ß╗út qu├í 2
- D. Sß╗æ phß╗®c c├│ phß║ºn thß╗▒c nß║▒m trong \(\left( { - 1;1} \right)\) v├á m├┤ ─æun kh├┤ng vã░ß╗út qu├í 2
-
- A. \(a^2+b^2\)
- B. \(a^2-b^2\)
- C. a+b
- D. a-b
-
- A. Ph├ó╠Çn thã░╠úc cu╠ëa z la╠Ç 2.
- B. Phần ảo của z là -2.
- C. S├┤╠ü phã░╠üc li├¬n hãí╠úp cu╠ëa z la╠Ç \(\overline z = - 2 + 2i\)
- D. \(\left| z \right| = \sqrt {{2^2} + {{\left( { - 2} \right)}^2}} = 2\sqrt 2 \)
-
- A. x = 3, y = 1
- B. x = 3, y = -1
- C. x = -3, y = -1
- D. x = -3, y = 1
-
- A. x = 2, y = -2
- B. x = -2, y = -2
- C. x = 2, y = 2
- D. x = -2, y = 2
-
- A. Hai điểm
- B. Hai ─æã░ß╗Øng thß║│ng
- C. ─Éã░ãí╠Çng tro╠Çn ba╠ün ki╠ünh R = 2
- D. ─Éã░ãí╠Çng tro╠Çn ba╠ün ki╠ünh R = \(\sqrt 2 \)