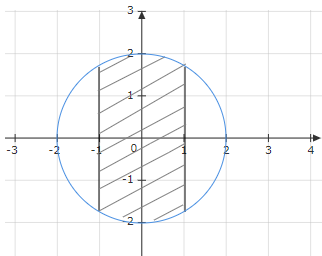
-
Câu hỏi:
Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo?
-
A.
Số phức có phần thực nằm trong \(\left( { - 1;1} \right)\) và mô đun nhỏ hơn 2
-
B.
Số phức có phần thực nằm trong \(\left[ { - 1;1} \right]\) và mô đun nhỏ hơn 2
-
C.
Số phức có phần thực nằm trong \(\left[ { - 1;1} \right]\) và mô đun không vượt quá 2
-
D.
Số phức có phần thực nằm trong \(\left( { - 1;1} \right)\) và mô đun không vượt quá 2
Lời giải tham khảo:
Đáp án đúng: C
Vậy ở đây ta thấy nếu lấy một điểm bất kì trong phần gạch chéo là \(M\left( {a,b} \right)\) thì \(\left\{ \begin{array}{l} - 1 \le a \le 1\\ OM \le 2 \end{array} \right.\)
Vậy đáp án là C.
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho số phức \(z = ax + bi\,\left( {a,b \in R} \right)\), mệnh đề nào sau đây là sai?
- Tìm điểm biểu diễn của số phức \(z = 5 - 3i\) trên mặt phẳng phức.
- Mệnh đề nào dưới đây là mệnh đề sai?
- Xác định tập hợp các điểm trong hệ tọa độ vuông góc biểu diễn số phức z = x + iy thỏa mãn điều kiện |z|=2
- Số phức thỏa mãn điều kiện nào thì có điểm biểu diễn ở phần gạch chéo?
- Cho số phức z=a+bi . Số phức \(z^2\) có phần thực là :
- Cho số phức z = 2 – 2i. Tìm khẳng định sai
- Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4)I = (2x + y) + 2yi
- Hai số phức \({z_1} = x - 2i,{z_2} = 2 + yi\,\left( {x,y \in R} \right)\) là liên hợp của nhau khi
- Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là