Xin chào các bạn đến với bài học thú vị trong sách Toán 11 Chân trời sáng tạo - Đường thẳng và mặt phẳng song song. Đừng lo lắng nếu bạn cảm thấy mình đang lạc bước trong một thế giới song song này. HOC247 sẽ chỉ bạn cách phân biệt giữa các đường thẳng và mặt phẳng song song trong không gian ba chiều, và làm thế nào để nhận ra chúng khi chúng đang bắt mắt chúng ta từ trên cao hoặc từ xa.
Tóm tắt lý thuyết
1.1. Đường thẳng song song với mặt phẳng
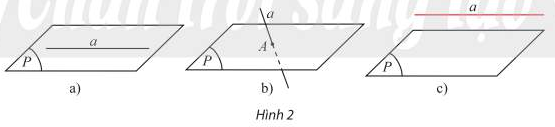
Cho đường thẳng a và mặt phẳng (P). Khi đó có thể xảy ra một trong ba trường hợp sau:
– Trường hợp 1: a và (P) có từ hai điểm chung phân biệt trở lên (Hình 2a), suy ra mọi điểm thuộc a đều thuộc (P), ta nói a nằm trong (P), kí hiệu a \(\\subset\) (P).
– Trường hợp 2: a và (P) có một điểm chung duy nhất 4 (Hình 2b), ta nói a cắt (P) tại A, kí hiệu a \(\cap\) (P) = A.
– Trường hợp 3: a và (P) không có điểm chung nào (Hình 2c), ta nói a song song với (P), kí hiệu a // (P).
|
Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung. |
1.2. Điều kiện để một đường thẳng song song với một mặt phẳng
Định lý 1:
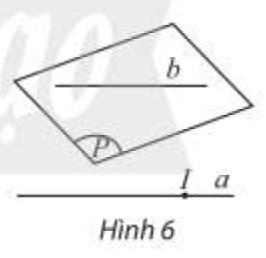
Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì a song song với (P).
1.3. Tính chất cơ bản của đường thẳng và mặt phẳng song song
Định lý 2:
Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a, cắt (P) theo giao tuyến b thì a song song với b
Từ Định lý 2, ta có các hệ quả sau:
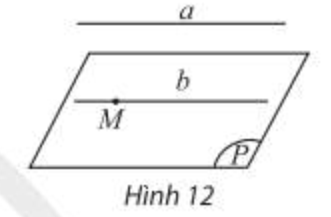
Hệ quả 1
Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thắng 6 song song với a thị 6 phải nằm trong (P).
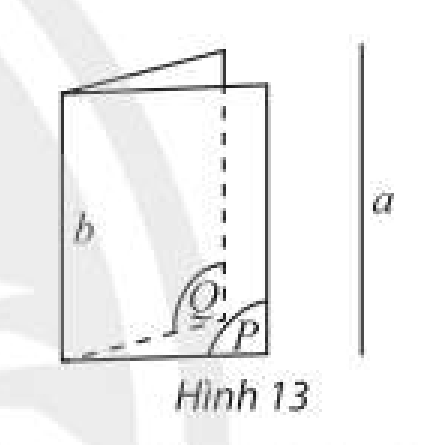
Hệ quả 2
Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Mặt phẳng đi qua một trong hai đường thẳng chéo nhau và song song với đường còn lại.
Định lý 3:
Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.
Bài tập minh họa
Câu 1: Cho tứ diện ABCD, gọi G là trọng tâm tam giác ACD, M thuộc đoạn thẳng BC sao cho CM = 2MB. Chọn mệnh đề đúng trong các mệnh đề sau?
A. MG // (ABC)
B. MG // (ABD)
C. MG // CD
D. MG // BD
Hướng dẫn giải
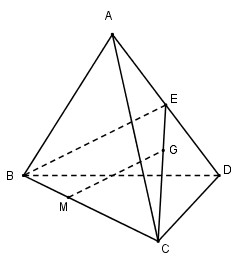
Gọi E là trung điểm của AD ta có \(G \in CE\) và \({{CG} \over {CE}} = {2 \over 3}\)
Vì \(CM = 2MB \Rightarrow {{CM} \over {CB}} = {2 \over 3}\)
Xét tam giác BCE có: \({{CG} \over {CE}} = {{CM} \over {CB}} = {2 \over 3} \Rightarrow \) MG // BE (Định lí Ta – let đảo)
Mà \(BE \subset \left( {ABD} \right) \Rightarrow \) MG // (ABD)
Chọn B.
Câu 2: Cho hình chóp S.ABCD. Gọi M, N lần lượt là trọng tâm của tam giác SAB và ABC. Khi đó MN song song với
A. mp(SAD)
B. AD
C. mp(SCD)
D. mp(SBD)
Hướng dẫn giải
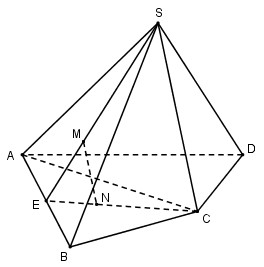
Gọi E là trung điểm của AB ta có:
\(\eqalign{ & M \in SE\,;\,{{EM} \over {ES}} = {1 \over 3} \cr & N \in EC\,;\,{{EN} \over {EC}} = {1 \over 3} \cr} \)
Xét tam giác ESC ta có \({{EM} \over {ES}} = {{EN} \over {EC}} = {1 \over 3} \Rightarrow \) MN // SC (Định lí Ta – let đảo).
Mà \(SC \subset \left( {SCD} \right) \Rightarrow \)MN // (SCD)
Chọn C.
Luyện tập Bài 3 Toán 11 Chân Trời Sáng Tạo
Học xong bài học này, em có thể:
- Nhận biết quan hệ song song giữa các đường thẳng và mặt phẳng.
- Vận dụng được các tính chất về quan hệ song song giữa các đường thẳng và mặt phẳng.
3.1. Trắc nghiệm Bài 3 Toán 11 Chân Trời Sáng Tạo
Các em có thể hệ thống lại nội dung kiến thức đã học được thông qua bài kiểm tra Trắc nghiệm Toán 11 Chân trời sáng tạo Chương 4 Bài 3 cực hay có đáp án và lời giải chi tiết.
-
- A. 3
- B. 1
- C. 2
- D. 4
-
- A. \(\left( ACD \right)\).
- B. \(\left( ABD \right)\).
- C. \(\left( ABC \right)\).
- D. \(\left( BCD \right)\).
-
- A. 3
- B. 2
- C. 4
- D. 1
Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức về bài học này nhé!
3.2. Bài tập SGK Bài 3 Toán 11 Chân Trời Sáng Tạo
Các em có thể xem thêm phần hướng dẫn Giải bài tập Toán 11 Chân trời sáng tạo Chương 4 Bài 3 để giúp các em nắm vững bài học và các phương pháp giải bài tập.
Hoạt động khởi động trang 107 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 1 trang 107 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 1 trang 108 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 2 trang 108 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 2 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 1 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 3 trang 109 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Hoạt động khám phá 4 trang 110 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Thực hành 3 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Vận dụng 2 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 1 trang 111 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 2 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 3 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 4 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 5 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Giải Bài 6 trang 112 SGK Toán 11 Chân trời sáng tạo tập 1 - CTST
Bài tập 1 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 2 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 3 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 4 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Bài tập 5 trang 122 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST
Hỏi đáp Bài 3 Toán 11 Chân Trời Sáng Tạo
Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán học HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!
Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!
-- Mod Toán Học 11 HỌC247