Bài tập 1 trang 121 SBT Toán 11 Tập 1 Chân trời sáng tạo - CTST

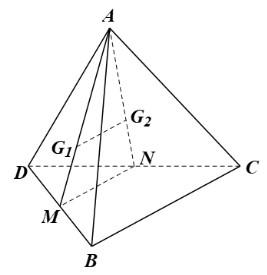
Gọi M, N lần lượt là trung điểm của DB, DC.

Xét ∆DBC có M, N lần lượt là trung điểm của DB, DC nên MN là đường trung bình của ∆DBC, suy ra MN // BC.

Do G₁ là trọng tâm ∆ABD nên $\frac{A{G}_1}{AM}=\frac{2}{3}$;

G₂ là trọng tâm ∆ACD nên $\frac{A{G}_2}{AN}=\frac{2}{3}$.

Do đó $\frac{A{G}_1}{AM}=\frac{A{G}_2}{AN}=\frac{2}{3}$.

Trong tam giác AMN, ta có $\frac{A{G}_1}{AM}=\frac{A{G}_2}{AN}=\frac{2}{3}$ nên G₁G₂ // MN (định lí Thalès đảo).

Mà MN // BC (chứng minh trên).

Suy ra G₁G₂ // MN // BC, mà BC ⊂ (ABC), MN ⊂ (BCD).

Suy ra G₁G₂ song song với các mặt phẳng (ABC) và (BCD).

-- Mod Toán 11 HỌC247