-
Câu hỏi:
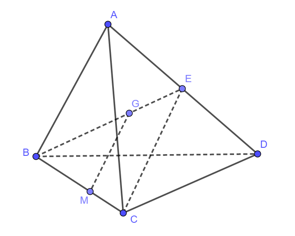
Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ABD\) và \(M\) là điểm trên cạnh \(BC\) sao cho \(BM=2MC\). Đường thẳng \(MG\) song song với mặt phẳng
-
A.
\(\left( ACD \right)\).
-
B.
\(\left( ABD \right)\).
-
C.
\(\left( ABC \right)\).
-
D.
\(\left( BCD \right)\).
Lời giải tham khảo:
Đáp án đúng: A
Chọn A
Gọi \(E\) là trung điểm \(AD\). Do \(G\) là trọng tâm của tam giác \(ABD\) và \(M\)là điểm trên cạnh\(BC\) sao cho \(BM=2MC\) nên trong mp\(\left( BCE \right)\) ta có: \(\frac{BG}{BE}=\frac{BM}{BC}=\frac{2}{3}\Rightarrow MG\parallel CE\subset \left( ACD \right)\Rightarrow MG\parallel \left( ACD \right)\).
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
QUẢNG CÁO
CÂU HỎI KHÁC
- Trong không gian, số vị trí tương đối giữa đường thẳng và mặt phẳng là?
- Cho tứ diện \(ABCD\). Gọi \(G\) là trọng tâm của tam giác \(ABD\) và \(M\) là điểm trên cạnh \(BC\) sao cho \(BM=2MC\)
- Cho hai đường thẳng \(a\) và \(b\) chéo nhau. Số mặt phẳng chứa \(a\) và song song với \(b\) là bao nhiêu?
- Cho mặt phẳng \(\left( P \right)\) và điểm \(A\) không thuộc mặt phẳng \(\left( P \right)\).
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành tâm \(O\), \(I\) là trung điểm cạnh \(SC\). Khẳng định nào sau đây SAI?
- Khẳng định nào sau đây đúng? Đường thẳng \(a\subset mp\left( P \right)\) và
- Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, \(AD\text{//}BC\), \(AD=2.BC\), \(M\) là trung điểm \(SA\).
- Cho tứ diện \(ABCD\) và \(M\) là điểm ở trên cạnh \(AC\). Mặt phẳng \(\left( \alpha \right)\) qua và \(M\) song song với \(AB\) và \(CD\).
- Cho mặt phẳng \(\left( \alpha \right)\) và đường thẳng \(d\not\subset \left( \alpha \right)\). Khẳng định nào sau đây sai?
- Cho hai đường thẳng \(a\) và \(b\) cùng song song với \(mp\left( P \right)\). Khẳng định nào sau đây không sai?
VIDEO
YOMEDIA
ADMICRO
