Vận dụng 1 trang 40 SGK Toán 10 Chân trời sáng tạo tập 2
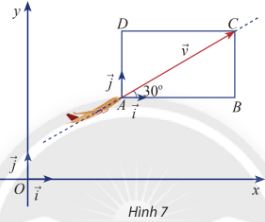
Một máy bay đang cất cánh với vận tốc 240 km/h theo phương hợp với phương nằm ngang một góc \(30^\circ \) (hình 7)
a) Tính độ dài mỗi cạnh của hình chữ nhật ABCD
b) Biểu diễn vận tốc \(\overrightarrow v \) theo hai vectơ và \(\overrightarrow j \)
c) Tìm tọa độ của \(\overrightarrow v \)
Hướng dẫn giải chi tiết Vận dụng 1
Phương pháp giải
+ Nếu \(\overrightarrow {OM} = \left( {x;y} \right)\) thì cặp số (x; y) là toa độ của điểm M, kí hiệu M(x; y), x gọi là hoành độ, y gọi là tung độ của điểm M
+ \(M\left( {x;y} \right) \Leftrightarrow \overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j \)
Chú ý: Hoành độ của điểm M còn được kí hiệu là xM, tung độ của điểm M còn được kí hiệu là yM. Khi đó ta việt M(xM; yM).
Lời giải chi tiết
a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\)
Áp dụng các tính chất trong tam giác vuông ta có
\(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120\frac{{\sqrt 3 }}{2}\)
\(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\)
b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120\frac{{\sqrt 3 }}{2}\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120\frac{{\sqrt 3 }}{2}\overrightarrow j \)
c) Ta có \(\overrightarrow v = 120\overrightarrow i + 120\frac{{\sqrt 3 }}{2}\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120\frac{{\sqrt 3 }}{2}} \right)\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Hoạt động khám phá 3 trang 39 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 1 trang 40 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 4 trang 40 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 2 trang 41 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 2 trang 41 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 5 trang 41 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 3 trang 42 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 6 trang 42 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 4 trang 43 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Hoạt động khám phá 7 trang 43 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Thực hành 5 trang 44 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Vận dụng 3 trang 44 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 1 trang 44 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 2 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 3 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 4 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 5 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 6 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 7 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 8 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 9 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 10 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải bài 11 trang 45 SGK Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 1 trang 58 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 2 trang 58 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 3 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 4 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 5 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 6 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 7 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 8 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 9 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 10 trang 59 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 11 trang 60 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
Giải Bài 12 trang 60 SBT Toán 10 Chân trời sáng tạo tập 2 - CTST
-


Hãy tìm các cặp số thực a và b sao cho cặp vecto sau bằng nhau: \(\overrightarrow x = \left( {a + b; - 2a + 3b} \right)\) và \(\overrightarrow y = \left( {2a - 3;4b} \right)\)
bởi Phong Vu
 18/09/2022
Theo dõi (0) 1 Trả lời
18/09/2022
Theo dõi (0) 1 Trả lời