Hoạt động 5 trang 86 SGK Toán 10 Cánh diều tập 1
Cho hai vecto \(\overrightarrow a \),\(\overrightarrow b \). Lấy một điểm M tùy ý.
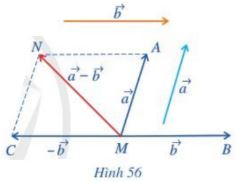
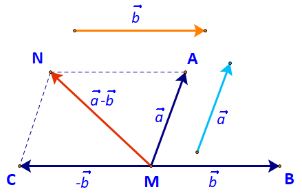
a) Vẽ \(\overrightarrow {MA} = \overrightarrow a ,\;\overrightarrow {MB} = \overrightarrow b ,\;\overrightarrow {MC} = - \overrightarrow b \) (Hình 56)
b) Tổng của hai vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) bằng vecto nào?
Hướng dẫn giải chi tiết Hoạt động 5
Phương pháp giải
a) Áp dụng kết quả: \(\overrightarrow {AB} = \overrightarrow {DC} \Leftrightarrow \)ABCD là hình bình hành. Để xác định các điểm A, B, C.
b) Đặt vecto \(\overrightarrow a \) và \(( - \overrightarrow b )\) vào hai vecto chung gốc là hai cạnh của một hình bình hành. Từ đó xác định tổng theo quy tắc hình bình hành.
Hướng dẫn giải
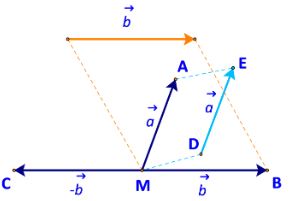
a) Đặt D, E lần lượt là điểm đầu và điểm cuối của vecto \(\overrightarrow a \).
Ta có: \(\overrightarrow {MA} = \overrightarrow a \)hay \(\overrightarrow {MA} = \overrightarrow {DE} \)
\( \Leftrightarrow MAED\) là hình bình hành.
Do đó A là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow a \)và điểm M.
Tương tự ta có:
B là đỉnh thứ tư của hình bình hành tạo bởi vecto \(\overrightarrow b \)và điểm M.
Lại có: \(\overrightarrow {MC} = - \overrightarrow b = - \overrightarrow {MB} \) do đó \(MC = MB\) và hai vecto \(\overrightarrow {MB} ,\overrightarrow {MC} \) ngược hướng nhau.
Hay M là trung điểm đoạn thẳng BC.
b) Lấy N là đỉnh thứ tư của hình bình hành AMCN.
Khi đó ta có: \(\overrightarrow {MA} + \overrightarrow {MC} = \overrightarrow {MN} \)
Mà: \(\overrightarrow {MA} = \overrightarrow a ;\;\overrightarrow {MC} = - \overrightarrow b \)
\( \Rightarrow \overrightarrow a + ( - \overrightarrow b ) = \overrightarrow {MN} \).
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Luyện tập 3 trang 85 SGK Toán 10 Cánh diều tập 1 - CD
Hoạt động 4 trang 85 SGK Toán 10 Cánh diều tập 1 - CD
Luyện tập 4 trang 86 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 1 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 2 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 3 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 4 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 5 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 6 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 7 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 8 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 9 trang 87 SGK Toán 10 Cánh diều tập 1 - CD
Giải bài 32 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 33 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 34 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 35 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 36 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 37 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 38 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 39 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 40 trang 92 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 41 trang 93 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 42 trang 93 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 43 trang 93 SBT Toán 10 Cánh diều tập 1 - CD
Giải bài 44 trang 93 SBT Toán 10 Cánh diều tập 1 - CD
-


Cho bốn điểm bất kì \(M, N, P, Q\). Chứng minh đẳng thức cho sau: \(\overrightarrow {NP} + \overrightarrow {MN} = \overrightarrow {QP} + \overrightarrow {MQ} \)
bởi Hoang Vu
 04/09/2022
Theo dõi (0) 1 Trả lời
04/09/2022
Theo dõi (0) 1 Trả lời