Giải bài 1 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1
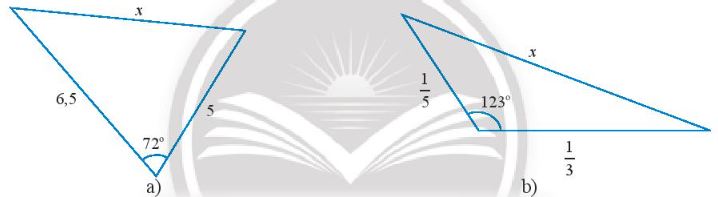
Tính độ dài cạnh x trong các tam giác sau:
Hướng dẫn giải chi tiết Bài 1
Phương pháp giải
Áp dụng định lí cosin, tính x bằng công thức: \({x^2} = 6,{5^2} + {5^2} - 2.6,5.5.\cos {72^o}\)
Lời giải chi tiết
a) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{x^2} = 6,{5^2} + {5^2} - 2.6,5.5.\cos {72^o} \approx 47,16\\ \Leftrightarrow x \approx 6,87\end{array}\)
b) Áp dụng định lí cosin, ta có:
\(\begin{array}{l}{x^2} = {\left( {\frac{1}{5}} \right)^2} + {\left( {\frac{1}{3}} \right)^2} - 2.\frac{1}{5}.\frac{1}{3}.\cos {123^o} \approx 0,224\\ \Leftrightarrow x \approx 0,473\end{array}\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Thực hành 3 trang 71 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Vận dụng 3 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 72 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Tính giá trị \(α\), biết: \(\sinα = 0\)
bởi Nhật Mai
 30/08/2022
Theo dõi (0) 1 Trả lời
30/08/2022
Theo dõi (0) 1 Trả lời