Giải bài 8 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1
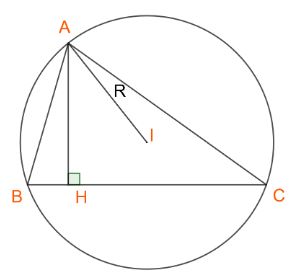
Cho \({h_a}\) là đường cao vẽ từ đỉnh A, R là bán kính đường tròn ngoại tiếp tam giác ABC. Chứng minh hệ thức: \({h_a} = 2R\sin B\sin C.\)
Hướng dẫn giải chi tiết Bài 8
Phương pháp giải
Bước 1: Tính \({h_a}\) theo b và sinC
Bước 2: Tính b theo R và sinB. Từ đó suy ra điều phải chứng minh.
Lời giải chi tiết
Đặt \(a = BC,b = AC,c = AB\)
Ta có: \(\sin C = \frac{{AH}}{{AC}} = \frac{{{h_a}}}{b} \Rightarrow {h_a} = b.\sin C\)
Theo định lí sin, ta có: \(\frac{b}{{\sin B}} = 2R \Rightarrow b = 2R.\sin B\)
\( \Rightarrow {h_a} = 2R.\sin B.\sin C\)
-- Mod Toán 10 HỌC247
Bài tập SGK khác
Giải bài 6 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 73 SGK Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 1 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 2 trang 74 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 3 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 4 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 5 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 6 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 7 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 8 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 9 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
Giải bài 10 trang 75 SBT Toán 10 Chân trời sáng tạo tập 1 - CTST
-


Thực hiện tính: \(\tan \frac{{31\pi }}{6}\)
bởi Trung Phung
 29/08/2022
Theo dõi (0) 1 Trả lời
29/08/2022
Theo dõi (0) 1 Trả lời