Phбә§n hЖ°б»ӣng dбә«n giбәЈi bГ i tбәӯp ToГЎn 10 Г”n tбәӯp chЖ°ЖЎng II HГ m sб»‘ bбәӯc nhбәҘt vГ bбәӯc hai sбәҪ giГәp cГЎc em nбәҜm Д‘Ж°б»Јc phЖ°ЖЎng phГЎp vГ rГЁn luyб»Үn kД© nДғng cГЎc giбәЈi bГ i tбәӯp tб»« SGK ДҗбәЎi sб»‘ 10 CЖЎ bбәЈn vГ NГўng cao.
-
BГ i tбәӯp 1 trang 50 SGK ДҗбәЎi sб»‘ 10
PhГЎt biб»ғu quy Ж°б»ӣc vб»Ғ xГЎc Д‘б»Ӣnh của hГ m sб»‘ cho bб»ҹi cГҙng thб»©c. Tб»« Д‘Гі hai hГ m sб»‘ \(y = \frac{{x + 1}}{{(x + 1)({x^2} + 2)}}\) vГ \(y = \frac{1}{{{x^2} + 2}}\) cГі gГ¬ khГЎc nhau?
-
BГ i tбәӯp 2 trang 50 SGK ДҗбәЎi sб»‘ 10
Thбәҝ nГ o lГ hГ m sб»‘ Д‘б»“ng biбәҝn (nghб»Ӣch biбәҝn) trГӘn khoбәЈng (a; b)?
-
BГ i tбәӯp 3 trang 50 SGK ДҗбәЎi sб»‘ 10
Thбәҝ nГ o lГ mб»ҷt hГ m sб»‘ chбәөn? Thбәҝ nГ o lГ mб»ҷt hГ m sб»‘ lбә»?
-
BГ i tбәӯp 4 trang 50 SGK ДҗбәЎi sб»‘ 10
Chб»ү ra khoбәЈng Д‘б»“ng biбәҝn, khoбәЈng nghб»Ӣch biбәҝn của hГ m sб»‘ y = ax + b, trong mб»—i trЖ°б»қng hб»Јp a > 0; a < 0.
- VIDEOYOMEDIA
-
BГ i tбәӯp 5 trang 50 SGK ДҗбәЎi sб»‘ 10
Chб»ү ra khoбәЈng Д‘б»“ng biбәҝn, khoбәЈng nghб»Ӣch biбәҝn của hГ m sб»‘: \(y = {\rm{a}}{{\rm{x}}^2} + bx + c,\) trong mб»—i trЖ°б»қng hб»Јp a > 0, a < 0.
-
BГ i tбәӯp 6 trang 50 SGK ДҗбәЎi sб»‘ 10
XГЎc Д‘б»Ӣnh toбәЎ Д‘б»ҷ của Д‘б»үnh, phЖ°ЖЎng trГ¬nh của trб»Ҙc Д‘б»‘i xб»©ng của parabol \(y = {\rm{a}}{{\rm{x}}^2} + bc + c.\)
-
BГ i tбәӯp 7 trang 50 SGK ДҗбәЎi sб»‘ 10
XГЎc Д‘б»Ӣnh toбәЎ Д‘б»ҷ giao Д‘iб»ғm của parabol \(y = {\rm{a}}{{\rm{x}}^2} + bc + c\) vб»ӣi trб»Ҙc tung. TГ¬m Д‘iб»Ғu kiб»Үn Д‘б»ғ parabol nГ y cбәҜt trб»Ҙc hoГ nh tбәЎi hai Д‘iб»ғm phГўn biб»Үt, tбәЎi mб»ҷt Д‘iб»ғm vГ viбәҝt toбәЎ Д‘б»ҷ của cГЎc giao Д‘iб»ғm trong mб»—i trЖ°б»қng hб»Јp.
-
BГ i tбәӯp 8 trang 50 SGK ДҗбәЎi sб»‘ 10
TГ¬m tбәӯp xГЎc Д‘б»Ӣnh của cГЎc hГ m sб»‘
a) \(y = \frac{2}{{x + 1}} + \sqrt {x + 3} \)
b) \(y = \sqrt {2 - 3x} - \frac{1}{{\sqrt {1 - 2x} }}\)
c) \(y = \left\{ \begin{array}{l}\frac{1}{{x + 3}}\,\,\,\,\,\,\,\,\,\,\,\,\,voi\,\,\,\,x \ge 1\\\sqrt {2 - x} \,\,\,\,\,\,\,\,\,voi\,x < 1\end{array} \right.\)
-
BГ i tбәӯp 9 trang 50 SGK ДҗбәЎi sб»‘ 10
KhбәЈo sГЎt sб»ұ biбәҝn thiГӘn vГ vбәҪ Д‘б»“ thб»Ӣ cГЎc hГ m sб»‘ sau:
a) \(y = \frac{1}{2}x - 1\) b) \(y = 4 - 2x\)
c) \(y = \sqrt {{x^2}} \) d) \(y = \left| {x + 1} \right|\)
-
BГ i tбәӯp 10 trang 51 SGK ДҗбәЎi sб»‘ 10
Lбәӯp bбәЈng biбәҝn thiГӘn vГ vбәҪ Д‘б»“ thб»Ӣ của cГЎc hГ m sб»‘
a) \(y = {x^2} - 2x - 1;\)
b) \(y = - {x^2} + 3x + 2\)
-
BГ i tбәӯp 11 trang 51 SGK ДҗбәЎi sб»‘ 10
XГЎc Д‘б»Ӣnh a, b biбәҝt Д‘Ж°б»қng thбәіng y = ax + b Д‘i qua hai Д‘iб»ғm A(1; 3), B(-1; 5).
-
BГ i tбәӯp 12 trang 51 SGK ДҗбәЎi sб»‘ 10
XГЎc Д‘б»Ӣnh a, b, c biбәҝt parabol \(y = {\rm{a}}{{\rm{x}}^2} + bx + c\)
a) Дҗi qua ba Д‘iб»ғm A(0; -1), B(1; -1); C(-1; 1)
b) CГі Д‘б»үnh I(1; 4) vГ Д‘i qua Д‘iб»ғm D(3; 0).
-
BГ i tбәӯp 2.27 trang 42 SBT ToГЎn 10
Hai hГ m sб»‘ y = x+4 vГ \(y = \frac{{{x^2} - 16}}{{x - 4}}\) cГі chung mб»ҷt tбәӯp xГЎc Д‘б»Ӣnh hay khГҙng ?
-
BГ i tбәӯp 2.28 trang 42 SBT ToГЎn 10
Cho hГ m sб»‘ y = f(x) nghб»Ӣch biбәҝn trГӘn khoбәЈng (a;b), khi Д‘Гі hГ m sб»‘ y = вҲ’f(x)cГі chiб»Ғu biбәҝn thiГӘn nhЖ° thбәҝ nГ o trГӘn khoбәЈng (a;b)?
-
BГ i tбәӯp 2.29 trang 43 SBT ToГЎn 10
Lбәӯp bбәЈng biбәҝn thiГӘn vГ vбәҪ Д‘б»“ thб»Ӣ hГ m sб»‘ y = x2вҲ’2|x|+1.
-
BГ i tбәӯp 2.30 trang 43 SBT ToГЎn 10
VбәҪ Д‘б»“ thб»Ӣ của hГ m sб»‘ \(y = \left| {\frac{2}{3}{x^2} - \frac{8}{3}x + 2} \right|\)
-
BГ i tбәӯp 2.31 trang 43 SBT ToГЎn 10
Cho hГ m sб»‘
\(y = f\left( x \right) = \left\{ \begin{array}{l}
\frac{2}{3}{x^2} - \frac{8}{3}x + 2,x > 0\\
2x + 2,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,x \le 0
\end{array} \right.\)VбәҪ Д‘б»“ thб»Ӣ của hГ m sб»‘ y=|f(x)|
-
BГ i tбәӯp 2.32 trang 43 SBT ToГЎn 10
Giao Д‘iб»ғm của parabol y = x2+4xвҲ’6 vГ Д‘Ж°б»қng thбәіng y = 2x+2 lГ
A. (2;6) vГ (3;8)
B. (вҲ’4;вҲ’6) vГ (1;вҲ’1)
C. (1;вҲ’1) vГ (2;6)
D. (вҲ’4;вҲ’6) vГ (2;6)
-
BГ i tбәӯp 2.33 trang 43 SBT ToГЎn 10
Tбәӯp xГЎc Д‘б»Ӣnh của hГ m sб»‘ \(y = \sqrt x + \frac{{{x^2} - 25}}{{x - 5}}\)
A. R
B. \(\left[ {0; + \infty } \right)\)
C. \(\left[ {0; + \infty } \right)\backslash \left\{ 5 \right\}\)
D. \(\left[ {0;5} \right)\)
-
BГ i tбәӯp 39 trang 63 SGK ToГЎn 10 NC
Vб»ӣi mб»—i cГўu sau Д‘Гўy. HГЈy chб»Қn phбә§n kбәҝt luбәӯn mГ em cho lГ Д‘Гәng:
a) TrГӘn khoбәЈng (-1; 1), hГ m sб»‘ y = - 2x + 5
(A) Дҗб»“ng biбәҝn
(B) Nghб»Ӣch biбәҝn;
(C) CбәЈ kбәҝt luбәӯn (A) vГ (B) Д‘б»Ғu sai.
b) TrГӘn khoбәЈng (0; 1), hГ m sб»‘ y = x2 + 2x - 3
(A) Дҗб»“ng biбәҝn
(B) Nghб»Ӣch biбәҝn;
(C) CбәЈ kбәҝt luбәӯn (A) vГ (B) Д‘б»Ғu sai.
c) TrГӘn khoбәЈng (- 2; 1) hГ m sб»‘ y = x2 + 2x - 3
(A) Дҗб»“ng biбәҝn
(B) Nghб»Ӣch biбәҝn;
(C) CбәЈ kбәҝt luбәӯn (A) vГ (B) Д‘б»Ғu sai.
-
BГ i tбәӯp 40 trang 63 SGK ToГЎn 10 NC
a) TГ¬m cГЎc hГ m sб»‘ lбә» trong cГЎc hГ m sб»‘ bбәӯc nhбәҘt \(y=ax+b\)
b) TГ¬m cГЎc hГ m sб»‘ chбә«n trong cГЎc hГ m sб»‘ bбәӯc hai \(y=ax^2+bx+c\)
-
BГ i tбәӯp 41 trang 63 SGK ToГЎn 10 NC
Dб»ұa vГ o Д‘б»“ thб»Ӣ của hГ m sб»‘ \(y=ax^2+bx+c\). HГЈy xГЎc Д‘б»Ӣnh dбәҘu của cГЎc hб»Ү sб»‘ a, b vГ c trong mб»—i trЖ°б»қng hб»Јp dЖ°б»ӣi Д‘Гўy:
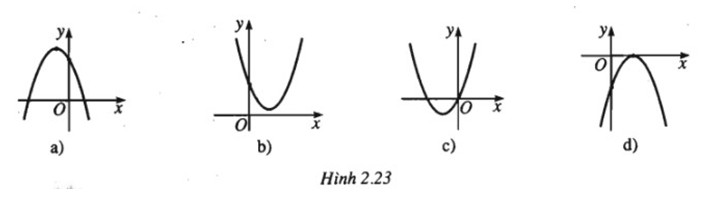
-
BГ i tбәӯp 42 trang 63 SGK ToГЎn 10 NC
Trong mб»—i trЖ°б»қng hб»Јp cho dЖ°б»ӣi Д‘Гўy, hГЈy vбәҪ Д‘б»“ thб»Ӣ hГ m sб»‘ của cГЎc hГ m sб»‘ trГӘn cГ№ng mб»ҷt hб»Ү trб»Ҙc tб»Қa Д‘б»ҷ rб»“i xГЎc Д‘б»Ӣnh tб»Қa Д‘б»ҷ giao Д‘iб»ғm của chГәng.
a) \(y=x-1\) vГ \(y=x^2-2x-1\)
b) \(y=-x+3\) vГ \(y=-x^2-4x+1\)
c) \(y=2x-5\) vГ \(y=x^2-4x-1\)
-
BГ i tбәӯp 43 trang 63 SGK ToГЎn 10 NC
XГЎc Д‘б»Ӣnh cГЎc hб»Ү sб»‘ a, b vГ c Д‘б»ғ cho hГ m sб»‘ \(y=ax^2+bx+c\) Д‘бәЎt giГЎ trб»Ӣ nhб»Ҹ nhбәҘt bбәұng \(\frac{3}{4}\) khi \(x = \frac{1}{2}\) vГ nhбәӯn giГЎ trб»Ӣ bбәұng 1 khi x = 1. Lбәӯp bбәЈng biбәҝn thiГӘn vГ vбәҪ Д‘б»“ thб»Ӣ của hГ m sб»‘.
-
BГ i tбәӯp 44 trang 64 SGK ToГЎn 10 NC
VбәҪ Д‘б»“ thб»Ӣ của cГЎc hГ m sб»‘ sau rб»“i lбәӯp bбәЈng biбәҝn thiГӘn của nГі
a) \(y = \left| {\frac{3}{2}x - 2} \right|\)
b) \(y = \left\{ \begin{array}{l}
2x,\,\,\,\,\,\,\,\,\,\,\,x < 0\\
{x^2} - x,\,\,\,\,x \ge 0
\end{array} \right.\)c) \(y = \left| {\frac{1}{2}{x^2} + x - \frac{3}{2}} \right|\)
d) \(y = x\left| x \right| - 2x - 1\)
a) \(y = \left| {\frac{3}{2}x - 2} \right|\)
b) \(y = \left\{ \begin{array}{l}
2x,\,\,\,\,\,\,\,\,\,\,\,x < 0\\
{x^2} - x,\,\,\,\,x \ge 0
\end{array} \right.\)c) \(y = \left| {\frac{1}{2}{x^2} + x - \frac{3}{2}} \right|\)
d) \(y = x\left| x \right| - 2x - 1\)
-
BГ i tбәӯp 45 trang 64 SGK ToГЎn 10 NC
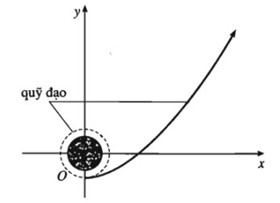
Khi mб»ҷt con tГ u vЕ© trб»Ҙ Д‘Ж°б»Јc phГіng lГӘn Mбә·t TrДғng, trЖ°б»ӣc hбәҝt nГі sбәҪ bay vГІng quanh TrГЎi ДҗбәҘt. Sau Д‘Гі, Д‘бәҝn mб»ҷt thб»қi Д‘iб»ғm thГӯch hб»Јp, Д‘б»ҷng cЖЎ bбәҜt Д‘бә§u hoбәЎt Д‘б»ҷng Д‘Ж°a con tГ u bay theo quб»№ Д‘бәЎo lГ mб»ҷt nhГЎnh hГ¬nh parabol lГӘn Mбә·t TrДғng (trong hб»Ү tб»Қa Д‘б»ҷ Oxy nhЖ° hГ¬nh vбәҪ bГӘn, X vГ y tГӯnh bбәұng nghГ¬n kilГҙmГ©t). Biбәҝt rбәұng khi Д‘б»ҷng cЖЎ bбәҜt Д‘бә§u hoбәЎt Д‘б»ҷng, x = 0 thГ¬ y = - 7. Sau Д‘Гі y = - 4 khi x = 10 vГ y = 5 khi x = 20.
a) TГ¬m hГ m sб»‘ cГі Д‘б»“ thб»Ӣ lГ nhГЎnh parabol nГіi trГӘn.
b) Theo lб»Ӣch trГ¬nh, Д‘бәҝ Д‘бәҝn Д‘Ж°б»Јc Mбә·t TrДғng, con tГ u phбәЈi Д‘i qua Д‘iб»ғm (100;V) vб»ӣi \(y = 294 \pm 1,5\). Hб»Ҹi Д‘iб»Ғu kiб»Үn Д‘Гі cГі Д‘Ж°б»Јc thб»Ҹa mГ n hay khГҙng?
-
BГ i tбәӯp 46 trang 64 SGK ToГЎn 10 NC
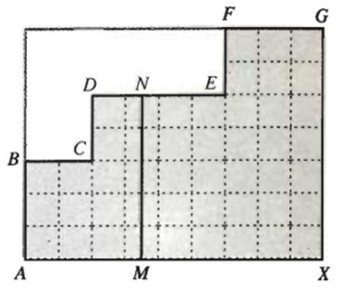
TrГӘn hГ¬nh bГӘn, Д‘iб»ғm M chuyб»ғn Д‘б»ҷng trГӘn Д‘oбәЎn thбәіng AX. Tб»« M, kбә» Д‘Ж°б»қng thбәіng song song vб»ӣi AB, cбәҜt mб»ҷt trong ba Д‘oбәЎn thбәіng BC, DE, FG tбәЎi Д‘iб»ғm N. Gб»Қi S lГ diб»Үn tГӯch của miб»Ғn tГҙ Д‘бәӯm nбәұm б»ҹ bГӘn trГЎi MN. Gб»Қi Д‘б»ҷ dГ i Д‘oбәЎn AM lГ x (0 < x < 9). Khi Д‘Гі S lГ mб»ҷt hГ m sб»‘ của biбәҝn x. HГЈy nГӘu biб»ғu thб»©c xГЎc Д‘б»Ӣnh hГ m sб»‘ S(x).