Toán 10 Kết nối tri thức Bài tập cuối chương 3

a) Giá trị lượng giác của một góc

Ta có các công thức sau:

\(\tan \alpha  = \frac{{\sin \alpha }}{{cos\alpha }}(\alpha  \ne {90^0});\cot \alpha  = \frac{{cos\alpha }}{{\sin \alpha }}(\alpha  \ne {0^0}\) và \(\alpha  \ne {180^0});\)

\(\tan \alpha  = \frac{1}{{\cot \alpha }}\left( {\alpha  \notin \left\{ {{0^0};{{90}^0};{{180}^0}} \right\}} \right)\)

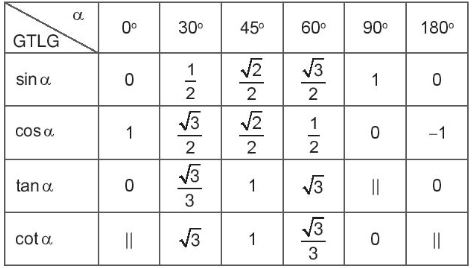
Sau đây là bảng giá trị lượng giác (GTLG) của một số góc đặc biệt mà em nên nhớ.

Đối với hai góc bù nhau, \(\alpha \) và \({{{180}^0} - \alpha }\), ta có:

\(\begin{array}{l}
*\sin \left( {{{180}^0} - \alpha } \right) = \sin \alpha ;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;*cos\left( {{{180}^0} - \alpha } \right) =  - cos\alpha \\
*\tan \left( {{{180}^0} - \alpha } \right) =  - \tan \left( {x \ne {{90}^0}} \right);\;\;\;\;\;\;\;\;\;*\cot \left( {{{180}^0} - \alpha } \right) =  - \cot \alpha \left( {{0^0} < \alpha  < {{180}^0}} \right)
\end{array}\)

a) Định lí Côsin

Trong tam giác ABC:

\(\begin{array}{l}
{a^2} = {b^2} + {c^2} - 2bc\cos A,\\
{b^2} = {c^2} + {a^2} - 2ca\cos B,\\
{c^2} = {a^2} + {b^2} - 2ab\cos C.
\end{array}\)

b) Định lí Sin

Trong tam giác ABC: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\)

c) Giải tam giác và ứng dụng thực tế

Việc tính độ dài các cạnh và số đo các góc của một tam giác khi biết một số yếu tố của tam giác đó được gọi là giải tam giác.

Chú ý: Áp dụng các định li côsin, sin và sử dụng máy tính cằm tay, ta có thể tính (gần đúng) các cạnh và các góc của một tam giác trong các trường hợp sau:

• Biết hai cạnh và góc xen giữa;
• Biết ba cạnh;
• Biết một cạnh và hai góc kề.

d) Công thức tính diện tích tam giác

\(\begin{array}{l}
*S = pr = \frac{{\left( {a + b + c} \right)r}}{2}\\
*S = \frac{1}{2}bc\sin A = \frac{1}{2}casinB = \frac{1}{2}ab\sin C\\
*S = \frac{{abc}}{{4R}}\\
*\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} 
\end{array}\)

Câu 1: Cho tam giác \(ABC\) biết các cạnh \(a = 52, 1cm\); \(b = 85cm\) và \(c = 54cm\). Tính các góc \(\widehat{A}\), \(\widehat{B}\), \(\widehat{C}\).

Hướng dẫn giải

Áp dụng định lí cosin: \({a^2} = {b^2} + {c^2} - 2bc.cosA.\)

Ta suy ra \(\cos A = \dfrac{b^{2}+c^{2}-a^{2}}{2bc}\)

\(= \dfrac{85^{2}+54^{2}-(52,1)^{2}}{2.85.54}\)

\(\Rightarrow \cos A  ≈ 0,809  \Rightarrow \widehat{A}≈ 36^0\) 

\(\begin{array}{l}
{b^2} = {c^2} + {a^2} - 2ca\cos B\\
\Rightarrow \cos B = \frac{{{c^2} + {a^2} - {b^2}}}{{2ca}}\\
= \frac{{{{54}^2} + 52,{1^2} - {{85}^2}}}{{2.54.52,1}} \approx - 0,2834
\end{array}\)

\(\Rightarrow  \widehat{B}≈  106^0 28’\) ;

\(\widehat{C} = {180^0} - \left( {A + B} \right) \) \(\approx {180^0} - \left( {{{36}^0} + {{106}^0}28'} \right)≈  37^032’\).

Câu 2: Tính diện tích tam giác ABC có \(b = 2,\;\widehat B = {30^o},\;\widehat C = {45^o}\).

Hướng dẫn giải

Áp dụng định lí sin cho tam giác ABC ta có:

\(\frac{b}{{\sin B}} = \frac{c}{{\sin C}}\)

\( \Rightarrow c = \sin C.\frac{b}{{\sin B}} = \sin {45^o}.\frac{2}{{\sin {{30}^o}}} = 2\sqrt 2 \)

Lại có: \(\;\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {30^o} - {45^o} = {105^o}\)

Do đó diện tích tích S của tam giác ABC là:

\(S = \frac{1}{2}bc.\sin A = \frac{1}{2}.2.2\sqrt 2 .\sin {105^o} = 1 + \sqrt 3 .\)

Vậy diện tích tam giác ABC là \(1 + \sqrt 3 \).

Câu 3:

a) Nêu nhận xét về vị trí điểm M trên nửa đường tròn đơn vị trong mỗi trường hợp sau:

\(\begin{array}{l}\alpha  = {90^o};\\\alpha  < {90^o};\\\alpha  > {90^o}.\end{array}\)

b) Khi \({0^o} < \alpha  < {90^o}\), nêu mối quan hệ giữa \(\cos \alpha ,\;\sin \alpha \) với hoành độ và tung độ của điểm M.

Hướng dẫn giải

a) Khi \(\alpha  = {90^o}\), điểm M trùng với điểm C. (Vì \(\widehat {xOC} = \widehat {AOC} = {90^o}\))

Khi \(\alpha  < {90^o}\), điểm M thuộc vào cung AC (bên phải trục tung)

Khi \(\alpha  > {90^o}\), điểm M thuộc vào cung BC (bên trái trục tung)

b) Khi \({0^o} < \alpha  < {90^o}\) , ta có:

\(\begin{array}{l}\cos \alpha  = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha  = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)

Vì \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nên \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nên \({y_0} > 0\)

Vậy \(\cos \alpha \) là hoành độ \({x_0}\)của điểm M, \(\sin \alpha \) là tung độ \({y_0}\) của điểm M.

Qua bài giảng này giúp các em:

- Nắm được định nghĩa giá trị lượng giác của một góc bất kì từ đến và giá trị lượng giác của các góc đặc biệt từ đến

- Hiểu quan hệ giữa các giá trị lượng giác của hai góc bù nhau.

 - Định lý Côsin trong tam giác, cách chứng minh định lý côsin trong tam giác.

 - Nắm được cách tìm số đo các góc của tam giác khi biết độ dài 3 cạnh, nắm công thức tính độ dài đường trung tuyến trong tam giác.

Để cũng cố bài học xin mời các em cũng làm Bài kiểm tra Trắc nghiệm Toán 10 Kết nối tri thức Bài tập cuối chương 3 để kiểm tra xem mình đã nắm được nội dung bài học hay chưa.

• Câu 1:

  Trong các đẳng thức sau đây, đẳng thức nào là đúng?

  • A. \(\sin 150^{\circ}=-\frac{\sqrt{3}}{2}\)
  • B. \(\cos 150^{\circ}=\frac{\sqrt{3}}{2}\)
  • C. \( \tan 150^{\circ}=-\frac{1}{\sqrt{3}}\)
  • D. \(\cot 150^{\circ}=\sqrt{3}\)

• Câu 2:

  Khẳng định nào sau đây sai?

  • A. \(\sin 90{}^\circ <\sin 100{}^\circ .\)      
  • B. \(\cos 95{}^\circ >\cos 100{}^\circ .\)
  • C. \(\tan 85{}^\circ <\tan 125{}^\circ .\)
  • D. \(\cos 145{}^\circ >\cos 125{}^\circ .\)

• Câu 3:

  Cho biết \(\sin \frac{\alpha }{3}=\frac{3}{5}.\) Giá trị của \(P=3{{\sin }^{2}}\frac{\alpha }{3}+5{{\cos }^{2}}\frac{\alpha }{3}\) bằng bao nhiêu ?

  • A. \(P=\frac{105}{25}.\)
  • B. \(P=\frac{107}{25}\).
  • C. \(P=\frac{109}{25}.\)
  • D. \(P=\frac{111}{25}.\)

Câu 4-10: Mời các em đăng nhập xem tiếp nội dung và thi thử Online để củng cố kiến thức và nắm vững hơn về bài học này nhé!

Bên cạnh đó các em có thể xem phần hướng dẫn Giải bài tập Toán 10 Kết nối tri thức Bài tập cuối chương 3 để giúp các em nắm vững bài học và các phương pháp giải bài tập.

Giải bài 3.12 trang 44 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.13 trang 44 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.14 trang 44 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.15 trang 44 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.16 trang 44 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.17 trang 44 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.18 trang 45 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.19 trang 45 SGK Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.17 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.18 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.19 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.20 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.21 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.22 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.23 trang 40 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.24 trang 41 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.25 trang 41 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.26 trang 41 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.27 trang 41 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.28 trang 41 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.29 trang 41 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.30 trang 42 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.31 trang 42 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.32 trang 42 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.33 trang 42 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.34 trang 42 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.35 trang 42 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.36 trang 43 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.37 trang 43 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.38 trang 43 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.39 trang 43 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.40 trang 43 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.41 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.42 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.43 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.44 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.45 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.46 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Giải bài 3.47 trang 44 SBT Toán 10 Kết nối tri thức tập 1 - KNTT

Trong quá trình học tập nếu có thắc mắc hay cần trợ giúp gì thì các em hãy comment ở mục Hỏi đáp, Cộng đồng Toán HOC247 sẽ hỗ trợ cho các em một cách nhanh chóng!

Chúc các em học tập tốt và luôn đạt thành tích cao trong học tập!