Дҗб»ғ giГәp cГЎc em hб»Қc tбәӯp hiб»Үu quбәЈ mГҙn ToГЎn 10, Д‘б»ҷi ngЕ© Hб»ҢC247 Д‘ГЈ biГӘn soбәЎn vГ tб»•ng hб»Јp nб»ҷi dung bГ i GiГЎ trб»Ӣ lЖ°б»Јng giГЎc của mб»ҷt gГіc tб»« 0Лҡ Д‘бәҝn 180Лҡ. BГ i giбәЈng gб»“m kiбәҝn thб»©c cбә§n nhб»ӣ vб»Ғ giГЎ trб»Ӣ lЖ°б»Јng giГЎc của mб»ҷt gГіc, mб»‘i quan hб»Ү giб»Ҝa cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của hai gГіc bГ№ nhau... BГӘn cбәЎnh Д‘Гі cГІn cГі cГЎc bГ i tбәӯp minh hб»Қa cГі hЖ°б»ӣng dбә«n giбәЈi chi tiбәҝt, giГәp cГЎc em hб»Қc tбәӯp vГ củng cб»‘ thбәӯt tб»‘t kiбәҝn thб»©c. Mб»қi cГЎc em cГ№ng tham khбәЈo.
TГіm tбәҜt lГҪ thuyбәҝt
1.1. GiГЎ trб»Ӣ lЖ°б»Јng giГЎc của mб»ҷt gГіc
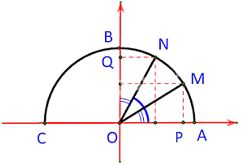
Trong mбә·t phбәіng toбәЎ Д‘б»ҷ Oxy, nб»ӯa Д‘Ж°б»қng trГІn tГўm O, bГЎn kГӯnh R = 1 nбәұm phГӯa trГӘn trб»Ҙc hoГ nh (HГ¬nh cho sau) Д‘Ж°б»Јc gб»Қi lГ nб»ӯa Д‘Ж°б»қng trГІn Д‘ЖЎn vб»Ӣ.
Cho trЖ°б»ӣc mб»ҷt gГіc \(\alpha\), \(0^\circ \le \alpha \le 180^\circ \). Khi Д‘Гі, cГі duy nhбәҘt Д‘iб»ғm M(x0; y0) trГӘn nб»ӯa Д‘Ж°б»қng trГІn Д‘ЖЎn vб»Ӣ nГіi trГӘn Д‘б»Ғ \(\widehat {xOM} = \alpha \).
Ta cГі cГЎc cГҙng thб»©c sau:
|
\(\tan \alpha = \frac{{\sin \alpha }}{{cos\alpha }}(\alpha \ne {90^0});\cot \alpha = \frac{{cos\alpha }}{{\sin \alpha }}(\alpha \ne {0^0}\) vГ \(\alpha \ne {180^0});\) \(\tan \alpha = \frac{1}{{\cot \alpha }}\left( {\alpha \notin \left\{ {{0^0};{{90}^0};{{180}^0}} \right\}} \right)\) |
|---|
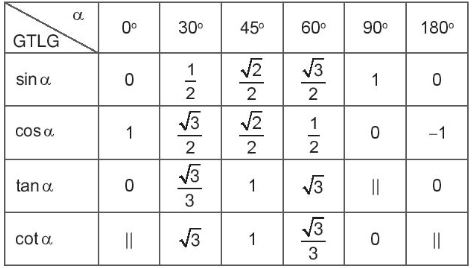
Sau Д‘Гўy lГ bбәЈng giГЎ trб»Ӣ lЖ°б»Јng giГЎc (GTLG) của mб»ҷt sб»‘ gГіc Д‘бә·c biб»Үt mГ em nГӘn nhб»ӣ.
ChГә ГҪ
- Khi tГ¬m x biбәҝt sin x, mГЎy tГӯnh chб»ү Д‘Ж°a ra giГЎ trб»Ӣ \(x \le {90^0}\).
- Muб»‘n tГ¬m x khi biбәҝt cos x, tan x, ta cЕ©ng lГ m tЖ°ЖЎng tб»ұ nhЖ° trГӘn, chб»ү thay phГӯm sin tЖ°ЖЎng б»©ng bб»ҹi phim cos , tan.
VГӯ dб»Ҙ: TГ¬m cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của gГіc 135В°.
GiбәЈi
Gб»Қi M lГ Д‘iб»ғm trГӘn nб»ӯa Д‘Ж°б»қng trГІn Д‘ЖЎn vб»Ӣ sao cho \(\widehat {xOM} = 135^\circ \). Gб»Қi N, P tЖ°ЖЎng б»©ng lГ hГ¬nh chiбәҝu vuГҙng gГіc của M lГӘn cГЎc trб»Ҙc Ox, Oy.
VГ¬ \(\widehat {xOM} = 135^\circ \) nГӘn \(\widehat {MON} = 45^\circ \), \(\widehat {MOP} = 45^\circ \). Vбәӯy cГЎc tam giГЎc MON, MOP lГ vuГҙng cГўn vб»ӣi cбәЎnh huyб»Ғn OM= 1.
Tб»« Д‘Гі, ta cГі \(ON = OP = \frac{{\sqrt 2 }}{2}\) Mбә·t khГЎc, Д‘iб»ғm M nбәұm bГӘn trГЎi trб»Ҙc tung nГӘn cГі toбәЎ Д‘б»ҷ lГ \(\left( { - \frac{{\sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)\).
Theo Д‘б»Ӣnh nghД©a, ta cГі:
\(\begin{array}{l}
\sin {135^0} = \frac{{\sqrt 2 }}{2};\;\;\;\;\;\;\;\;\;cos{135^0} = - \frac{{\sqrt 2 }}{2};\\
\tan {135^0} = - 1;\;\;\;\;\;\;\;\;\;\;\cot {135^0} = - 1
\end{array}\)
1.2. Mб»‘i quan hб»Ү giб»Ҝa cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của hai gГіc bГ№ nhau
б»һ lб»ӣp 9, em Д‘ГЈ biбәҝt mб»‘i quan hб»Ү giб»Ҝa tб»ү sб»‘ lЖ°б»Јng giГЎc của hai gГіc phб»Ҙ nhau. Trong mб»Ҙc nГ y, em hГЈy tГ¬m mб»‘i quan hб»Ү giб»Ҝa cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của hai gГіc bГ№ nhau.
Дҗб»‘i vб»ӣi mб»ҷt gГіc \(\alpha\) tuб»і ГҪ \({0^0} \le \alpha \le {180^0}\), gб»Қi M, M' lГ hai Д‘iб»ғm trГӘn nб»ӯa Д‘Ж°б»қng trГІn Д‘ЖЎn vб»Ӣ tЖ°ЖЎng б»©ng vб»ӣi hai gГіc bГ№ nhau \(\alpha\) vГ \({180^0} - \alpha \) \(\left( {\widehat {xOM} = \alpha ,\widehat {xOM'} = {{180}^0} - \alpha } \right)\)
|
Дҗб»‘i vб»ӣi hai gГіc bГ№ nhau, \(\alpha \) vГ \({{{180}^0} - \alpha }\), ta cГі: \(\begin{array}{l} |
|---|
VГӯ dб»Ҙ: TГӯnh cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của cГЎc gГіc 120В°,135В°,150В°.
GiбәЈi
Do cГЎc gГіc 120В°,135В°,150В° tЖ°ЖЎng б»©ng bГ№ vб»ӣi cГЎc gГіc 60В°,45В°,30В°, ta cЕ©ng cГі bбәЈng cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc sau:
BГ i tбәӯp minh hб»Қa
CГўu 1:
a) NГӘu nhбәӯn xГ©t vб»Ғ vб»Ӣ trГӯ Д‘iб»ғm M trГӘn nб»ӯa Д‘Ж°б»қng trГІn Д‘ЖЎn vб»Ӣ trong mб»—i trЖ°б»қng hб»Јp sau:
\(\begin{array}{l}\alpha = {90^o};\\\alpha < {90^o};\\\alpha > {90^o}.\end{array}\)
b) Khi \({0^o} < \alpha < {90^o}\), nГӘu mб»‘i quan hб»Ү giб»Ҝa \(\cos \alpha ,\;\sin \alpha \) vб»ӣi hoГ nh Д‘б»ҷ vГ tung Д‘б»ҷ của Д‘iб»ғm M.
HЖ°б»ӣng dбә«n giбәЈi
a) Khi \(\alpha = {90^o}\), Д‘iб»ғm M trГ№ng vб»ӣi Д‘iб»ғm C. (VГ¬ \(\widehat {xOC} = \widehat {AOC} = {90^o}\))
Khi \(\alpha < {90^o}\), Д‘iб»ғm M thuб»ҷc vГ o cung AC (bГӘn phбәЈi trб»Ҙc tung)
Khi \(\alpha > {90^o}\), Д‘iб»ғm M thuб»ҷc vГ o cung BC (bГӘn trГЎi trб»Ҙc tung)
b) Khi \({0^o} < \alpha < {90^o}\) , ta cГі:
\(\begin{array}{l}\cos \alpha = \frac{{\left| {{x_0}} \right|}}{{OM}} = \left| {{x_0}} \right| = {x_0};\\\sin \alpha = \frac{{\left| {{y_0}} \right|}}{{OM}} = \left| {{y_o}} \right| = {y_o}\end{array}\)
VГ¬ \(OM = R = 1\); \({x_0} \in \)tia \(Ox\)nГӘn \({x_0} > 0\); \({y_0} \in \)tia \(Oy\)nГӘn \({y_0} > 0\)
Vбәӯy \(\cos \alpha \) lГ hoГ nh Д‘б»ҷ \({x_0}\)của Д‘iб»ғm M, \(\sin \alpha \) lГ tung Д‘б»ҷ \({y_0}\) của Д‘iб»ғm M.
CГўu 2:
Trong hГ¬nh cho sau, hai Д‘iб»ғm M, N б»©ng vб»ӣi hai gГіc phб»Ҙ nhau \(\alpha \) vГ \({90^o} - \alpha \) (\(\widehat {xOM} = \alpha ,\;\;\widehat {xON} = {90^o} - \alpha \)). Chб»©ng mГ¬nh rбәұng \(\Delta MOP = \Delta NOQ\). Tб»« Д‘Гі nГӘu mб»‘i quan hб»Ү giб»Ҝa \(\cos \alpha \) vГ \(\sin \left( {{{90}^o} - \alpha } \right)\).
HЖ°б»ӣng dбә«n giбәЈi
TrЖ°б»қng hб»Јp 1: \(\alpha = {90^o}\)
Khi Д‘Гі \({90^o} - \alpha = {0^o}\)
Tб»©c lГ M vГ N lбә§n lЖ°б»Јt trГ№ng nhau vб»ӣi B vГ A.
VГ \(\cos \alpha = 0 = \sin \left( {{{90}^o} - \alpha } \right)\)
TrЖ°б»қng hб»Јp 2: \({0^o} < \alpha < {90^o} \Rightarrow {0^o} < {90^o} - \alpha < {90^0}\)
M vГ N cГ№ng nбәұm bГӘn trГЎi phбәЈi trб»Ҙc tung.
Ta cГі: \(\alpha = \widehat {AOM};\;\;{90^o} - \alpha = \widehat {AON}\)
Dб»… thбәҘy: \(\widehat {AON} = {90^o} - \alpha = {90^o} - \widehat {NOB}\;\;\; \Rightarrow \alpha = \widehat {NOB}\)
XГ©t hai tam giГЎc vuГҙng \(NOQ\) vГ tam giГЎc \(MOP\) ta cГі:
\(OM = ON\)
\(\widehat {POM} = \widehat {QON}\)
\(\begin{array}{l} \Rightarrow \Delta NOQ = \Delta MOP\\ \Rightarrow \left\{ \begin{array}{l}OP = OQ\\QN = MP\end{array} \right.\end{array}\)
MГ \(M\left( {{x_0};{y_o}} \right)\) nГӘn \(N\left( {{y_o};{x_0}} \right)\). NГіi cГЎch khГЎc:
\(\cos \left( {{{90}^o} - \alpha } \right) = \sin \alpha ;\;\;\sin \left( {{{90}^o} - \alpha } \right) = \cos \alpha .\)
Luyб»Үn tбәӯp BГ i 5 ToГЎn 10 KNTT
Qua bГ i giбәЈng trГӘn sбәҪ giГәp cГЎc em nбәҜm Д‘Ж°б»Јc cГЎc nб»ҷi dung nhЖ° sau:
- NбәҜm Д‘Ж°б»Јc Д‘б»Ӣnh nghД©a giГЎ trб»Ӣ lЖ°б»Јng giГЎc của mб»ҷt gГіc bбәҘt kГ¬ tб»« Д‘бәҝn vГ giГЎ trб»Ӣ lЖ°б»Јng giГЎc của cГЎc gГіc Д‘бә·c biб»Үt tб»« Д‘бәҝn
- Hiб»ғu quan hб»Ү giб»Ҝa cГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của hai gГіc bГ№ nhau
- Hiб»ғu khГЎi niб»Үm gГіc giб»Ҝa hai vectЖЎ, nбәҜm Д‘Ж°б»Јc cГЎch xГЎc Д‘б»Ӣnh gГіc giб»Ҝa hai vectЖЎ
3.1. BГ i tбәӯp trбәҜc nghiб»Үm BГ i 5 ToГЎn 10 KNTT
Дҗб»ғ cЕ©ng cб»‘ bГ i hб»Қc xin mб»қi cГЎc em cЕ©ng lГ m BГ i kiб»ғm tra TrбәҜc nghiб»Үm ToГЎn 10 Kбәҝt nб»‘i tri thб»©c ChЖ°ЖЎng 3 BГ i 5 Д‘б»ғ kiб»ғm tra xem mГ¬nh Д‘ГЈ nбәҜm Д‘Ж°б»Јc nб»ҷi dung bГ i hб»Қc hay chЖ°a.
-
CГўu 1:
Cho gГіc Оұ thб»Ҹa mГЈn \({0^o} < \alpha < {90^o}\). Khбәіng Д‘б»Ӣnh nГ o sau Д‘Гўy lГ Д‘Гәng?
- A. CГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của Оұ lГ cГЎc sб»‘ dЖ°ЖЎng
- B. CГЎc giГЎ trб»Ӣ lЖ°б»Јng giГЎc của Оұ lГ cГЎc sб»‘ Гўm
- C. sin Оұ vГ tan Оұ trГЎi dбәҘu
- D. cos Оұ vГ tan Оұ trГЎi dбәҘu
-
- A. 0
- B. 1
- C. -1
- D. 2
-
- A. \(\frac{\sqrt{5}}{2}\)
- B. \(\pm \frac{\sqrt{5}}{5}\)
- C. \(-\frac{\sqrt{5}}{5}\)
- D. \(-\frac{1}{3}\)
CГўu 4-10: Mб»қi cГЎc em Д‘Дғng nhбәӯp xem tiбәҝp nб»ҷi dung vГ thi thб»ӯ Online Д‘б»ғ củng cб»‘ kiбәҝn thб»©c vГ nбәҜm vб»Ҝng hЖЎn vб»Ғ bГ i hб»Қc nГ y nhГ©!
3.2. BГ i tбәӯp SGK BГ i 5 ToГЎn 10 KNTT
BГӘn cбәЎnh Д‘Гі cГЎc em cГі thб»ғ xem phбә§n hЖ°б»ӣng dбә«n GiбәЈi bГ i tбәӯp ToГЎn 10 Kбәҝt nб»‘i tri thб»©c ChЖ°ЖЎng 3 BГ i 5 Д‘б»ғ giГәp cГЎc em nбәҜm vб»Ҝng bГ i hб»Қc vГ cГЎc phЖ°ЖЎng phГЎp giбәЈi bГ i tбәӯp.
HoбәЎt Д‘б»ҷng 1 trang 34 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
Luyб»Үn tбәӯp 1 trang 35 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
HoбәЎt Д‘б»ҷng 2 trang 36 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
Luyб»Үn tбәӯp 2 trang 36 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
Vбәӯn dб»Ҙng trang 37 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.1 trang 37 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.2 trang 37 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.3 trang 37 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.4 trang 37 SGK ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.1 trang 32 SBT ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.2 trang 32 SBT ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.3 trang 33 SBT ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.4 trang 33 SBT ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.5 trang 34 SBT ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
GiбәЈi bГ i 3.6 trang 34 SBT ToГЎn 10 KГӘМҒt nГҙМҒi tri thЖ°МҒc tбәӯp 1 - KNTT
Hб»Ҹi Д‘ГЎp BГ i 5 ToГЎn 10 KNTT
Trong quГЎ trГ¬nh hб»Қc tбәӯp nбәҝu cГі thбәҜc mбәҜc hay cбә§n trб»Ј giГәp gГ¬ thГ¬ cГЎc em hГЈy comment б»ҹ mб»Ҙc Hб»Ҹi Д‘ГЎp, Cб»ҷng Д‘б»“ng ToГЎn HOC247 sбәҪ hб»— trб»Ј cho cГЎc em mб»ҷt cГЎch nhanh chГіng!
ChГәc cГЎc em hб»Қc tбәӯp tб»‘t vГ luГҙn Д‘бәЎt thГ nh tГӯch cao trong hб»Қc tбәӯp!
-- Mod ToГЎn Hб»Қc 10 Hб»ҢC247


.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)
.JPG)