-
Câu hỏi:
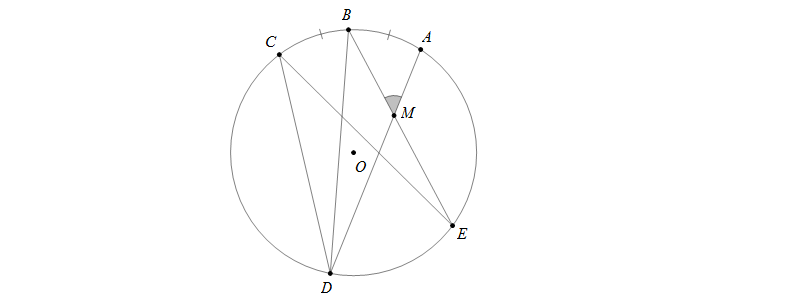
Dựa vào hình vẽ sau, biết B là điểm chính giữa cung nhỏ AC, M là giao điểm của AD và BE và sđ\(\stackrel\frown{BC}=30^0\), \(\widehat{DCE}=30^0\). Lúc đó \(\widehat{AMB}=?\)
-
A.
900
-
B.
600
-
C.
450
-
D.
500
Lời giải tham khảo:
Đáp án đúng: C

Vì B là điểm chính giữa cung AC nên sđ\(\stackrel\frown{BC}=\)sđ\(\stackrel\frown{AB}=30^0\).
Theo đề bài \(\widehat{DCE}=30^0\Rightarrow\) sđ\(\stackrel\frown{DE}=60^0\)
Khi đó \(\widehat{AMB}=\frac{1}{2}\)(sđ\(\stackrel\frown{AB}+\)sđ\(\stackrel\frown{DE}\))\(=\frac{1}{2}(30^0+60^0)=45^0\)
Hãy trả lời câu hỏi trước khi xem đáp án và lời giải -
A.
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, bấm vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Dựa vào hình vẽ sau, biết B là điểm chính giữa cung nhỏ AC, M là giao điểm của AD và BE và sđ stackrelfrown{BC}=30^0, DCE=30^0
- Khẳng nào sau đây là đúng:
- Số đo góc AED là bao nhiêu biết rằng widehat{OBC}=45^0,widehat{ABD}=15^0
- Cho đường tròn (O) và điểm E nằm ngoài đường tròn. Vẽ cát tuyến EAB và ECD với đường tròn (A nằm giữa E và B, C nằm giữa E và D)
- Cho đường tròn (O) và hai dây AB,CD của đường tròn sao cho AB cắt CD tại E. I là giao điểm của AD và BC

