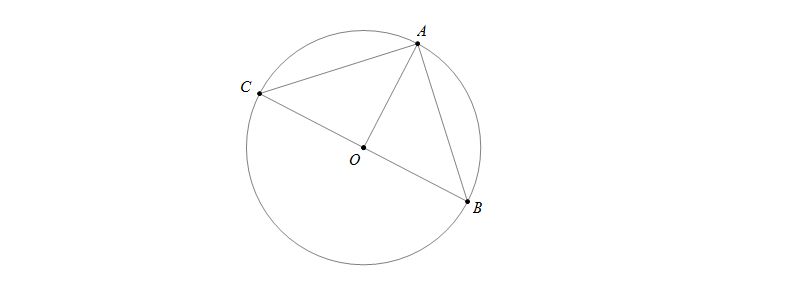
+ A là điểm chính giữa cung BC nên \(\stackrel\frown{AB}=\stackrel\frown{AC}\Rightarrow AB=AC \Rightarrow \bigtriangleup ABC\) cân tại A

Mặt khác O là trung điểm BC nên \(AO\perp BC\) (do đó ý D đúng)

+ Tam giác AOB vuông tại O nên \(AB>AO\) (từ đó ý A đúng)

+ Tam giác AOB vuông tại O có OA=OB nên tam giác AOB vuông cân tại O, suy ra \(\widehat{ABC}=45^0\) (ý C đúng)

+ Ngoài ra đường kính BC=20cm nên OB=10cm, suy ra OA=10cm

Áp dụng định lí Pytago cho tam giác vuông AOB ta có \(AB=\sqrt{AO^2+BO^2}=\sqrt{10^2+10^2}=10\sqrt{2} cm\) (ý B sai)
Kết luận: chọn câu B