Giải bài 7.2 tr 168 sách BT Toán lớp 9 Tập 1
Cho hai đường tròn \((O)\) và \((O')\) cắt nhau tại \(A\) và \(B.\) Một đường thẳng vuông góc với \(AB\) tại \(B\) cắt các đường tròn \((O)\) và \((O')\) theo thứ tự tại \(C\) và \(D\) ( khác \(B\)). Chứng minh rằng \(OO’ =\displaystyle {1 \over 2}CD\).
Hướng dẫn giải chi tiết
Hướng dẫn giải
Sử dụng kiến thức:
+) Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền.
+) Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy.
Lời giải chi tiết
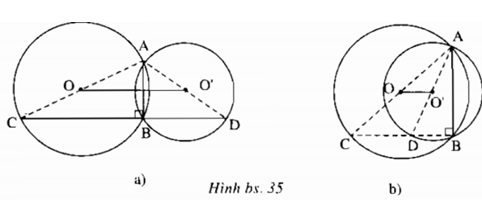
Vì \(\widehat {ABC} = 90^\circ \) nên tam giác ABC vuông tại B có O là tâm đường tròn ngoại tiếp, do đó \(A, O, C\) thẳng hàng.
Vì \(\widehat {ABD} = 90^\circ \) nên tam giác ABD vuông tại B có O' là tâm đường tròn ngoại tiếp, do đó \(A, O', D\) thẳng hàng.
Trong \(∆ACD\), có:
\(O\) là trung điểm của \(AC\)
\(O'\) là trung điểm của \(AD\)
\(\Rightarrow OO'\) là đường trung bình của \(∆ACD\) nên \(OO’ =\displaystyle {1 \over 2}CD\).
Chú ý: 2 trường hợp hình vẽ đều được chứng minh như trên.
-- Mod Toán 9 HỌC247
Bài tập SGK khác
Bài tập 70 trang 168 SBT Toán 9 Tập 1
Bài tập 7.1 trang 168 SBT Toán 9 Tập 1
Bài tập 71 trang 168 SBT Toán 9 Tập 1
Bài tập 72 trang 169 SBT Toán 9 Tập 1
Bài tập 73 trang 169 SBT Toán 9 Tập 1
Bài tập 74 trang 169 SBT Toán 9 Tập 1
Bài tập 75 trang 169 SBT Toán 9 Tập 1
Bài tập 76 trang 169 SBT Toán 9 Tập 1
Bài tập 77 trang 169 SBT Toán 9 Tập 1
Bài tập 78 trang 170 SBT Toán 9 Tập 1
Bài tập 79 trang 170 SBT Toán 9 Tập 1
Bài tập 80 trang 170 SBT Toán 9 Tập 1
Bài tập 8.1 trang 170 SBT Toán 9 Tập 1
-


Chứng minh tam giác CAI = tam giác CBN
bởi Nguyễn Lệ Diễm
 25/01/2019
25/01/2019
Cho nửa đường tròn tâm O, đường kính AB và 1 điểm I nằm giữa A và B. Gọi C là 1 điểm trên nửa đường tròn tâm O. Đường thẳng kẻ qua C vuông góc với IC cắt các tiếp tuyến của nửa đường tròn tại A và B lần lượt tại M và N
a. Chứng minh : Tam giác CAI = tam giác CBN
b. So sánh 2 tam giác ABC và INC
c. Chứng minh: góc MIN = 90 độ
Theo dõi (0) 1 Trả lời





