Bài tập 76 trang 169 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì điểm đó cách đều hai tiếp điểm.

+) Tứ giác có ba góc vuông là hình chữ nhật.

+) Trong hình chữ nhật, hai đường chéo cắt nhau tại trung điểm mỗi đường.

+) Nếu một đường thẳng đi qua một điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn.

Lời giải chi tiết

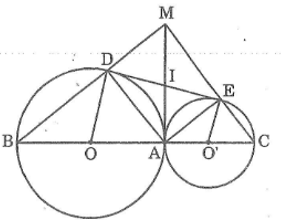
\(a)\) Kẻ tiếp tuyến chung tại \(A\) cắt \(DE\) tại \(I\)

Trong đường tròn \((O)\) ta có:

\(IA = ID\) (tính chất hai tiếp tuyến cắt nhau)

Trong đường tròn \((O’)\) ta có:

\(IA = IE\) (tính chất hai tiếp tuyến cắt nhau)

Suy ra: \(IA = ID = IE = \displaystyle {1 \over 2} DE\)

Tam giác \(ADE\) có đường trung tuyến \(AI\) ứng với cạnh \(DE\) và bằng nửa cạnh \(DE\) nên tam giác \(ADE\) vuông tại \(A.\)

Suy ra: \(\widehat {EAD} = 90^\circ \)

\(b)\) Tam giác \(ABD\) nội tiếp trong đường tròn \((O)\) có \(AB\) là đường kính nên \(\widehat {ADB} = 90^\circ \) hay \(AD\bot BM\), suy ra \(\widehat {ADM} = 90^\circ \)

Tam giác \(AEC\) nội tiếp trong đường tròn \((O')\) có \(AC\) là đường kính nên \(\widehat {AEC} = 90^\circ \) hay \(AE\bot CM\), suy ra \(\widehat {AEM} = 90^\circ \)

Mặt khác: \(\widehat {EAD} = 90^\circ \) (chứng minh trên)

Tứ giác \(ADME\) có ba góc vuông nên nó là hình chữ nhật.

\(c)\) Tứ giác \(ADME\) là hình chữ nhật và \(ID = IE\) (chứng minh trên) nên đường chéo \(AM\) của hình chữ nhật phải đi qua trung điểm \(I\) của \(DE.\) Suy ra: \(A, I, M\) thẳng hàng.

Ta có: \(IA ⊥ OO'\) ( vì \(IA\) là tiếp tuyến của \((O)\))

Suy ra: \(AM ⊥ OO'\)

Vậy \(MA\) là tiếp tuyến chung của đường tròn \((O)\) và \((O').\)

-- Mod Toán 9 HỌC247