Bài tập 8.3 trang 171 SBT Toán 9 Tập 1

Hướng dẫn giải

Sử dụng kiến thức:

+) Trong một đường tròn, đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy.

+) Nếu \(OO' = R – r\) thì đường tròn \((O)\) và đường tròn \((O')\) tiếp xúc trong.

+) Tâm đường tròn ngoại tiếp tam giác vuông là trung điểm cạnh huyền.

Lời giải chi tiết

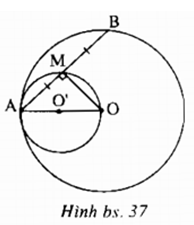
\(a)\) Xét đường tròn (O) có M là trung điểm của dây AB nên \(OM\bot AB\) (quan hệ giữa đường kính và dây cung)

Suy ra \(\widehat {AMO} = 90^\circ \) hay tam giác AMO vuông tại M.

Do đó, điểm \(M\) chuyển động trên đường tròn \((O')\) đường kính \(AO.\)

\(b)\) Ta có: \(OO'=OA-O'A\)

Vậy đường tròn \((O')\) tiếp xúc trong với đường tròn \((O).\)

-- Mod Toán 9 HỌC247